previous  home  next  PDF

23. Motion of a Rigid Body:  the Inertia Tensor

Michael Fowler

Definition of Rigid

We’re thinking here of an idealized solid, in which the distance between any two internal points stays the same as the body moves around.  That is, we ignore vibrations, or strains in the material resulting from inside or outside stresses.  In fact, this is almost always an excellent approximation for ordinary solids subject to typical stresses—obvious exceptions being rubber, flesh, etc.  Following Landau, we’ll usually begin by representing the body as a collection of particles of different masses $m_i$ held in their places ${\overrightarrow{r}}_i$ by massless bonds. This approach has the merit that the dynamics can be expressed cleanly in terms of sums over the particles, but for an ordinary solid we’ll finally take a continuum limit, replacing the finite sums over the constituent particles by integrals over a continuous mass distribution.

Rotation of a Body about a Fixed Axis

As a preliminary, let’s look at a body firmly attached to a rod fixed in space, and rotating with angular velocity $\Omega$ radians/sec. about that axis.  You’ll recall from freshman physics that the angular momentum and rotational energy are $L_z=I\Omega ,E_{\text{rot}}=\frac{1}{2}I{\Omega }^2$ where

$I={\displaystyle \sum _i{m}_i{r}_{\perp i}^2}={\displaystyle \int dxdydz\rho \left(x,y,z\right)r_{\perp }^2}$

(here $r_{\perp }=\sqrt{x^2+y^2}$ is the distance from the axis).

 

 

 

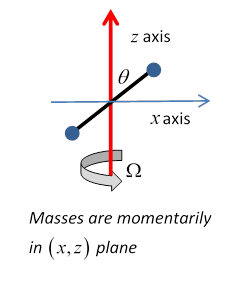
But you also know that both angular velocity and angular momentum are vectors. Obviously, for this example, the angular velocity is a vector pointing along the axis of rotation, $\overrightarrow{\Omega }=\left(0,0,{\Omega }_z\right).$ One might be tempted to conclude that the angular momentum also points along the axis, but this is not always the case. An instructive example is provided by two masses $m$ at the ends of a rod of length $2a$ held at a fixed angle $\theta$ to the $z$ axis, which is the axis of rotation.

Evidently,

$L_z=2m{a}^2{\sin }^2\theta \cdot \Omega .$

But notice that, assuming the rod is momentarily in the $xz$ plane, as shown, then

$L_x=-2m{a}^2{\cos }^2\theta \cdot \Omega .$

The total angular momentum is not parallel to the total angular velocity! 

In fact, as should be evident, the total angular momentum is rotating around the constant angular velocity vector, so the axis must be providing a torque. This is why unbalanced car wheels stress the axle.  

General Motion of a Rotating Rigid Body

We’ll follow the Landau notation (which itself tends to be bilingual between coordinates $\left(x,y,z\right)$ and $\left(x_1,x_2,x_3\right)$.)  Notice that we’ll label the components by $\left(x_1,x_2,x_3\right)$, not $\left(r_1,r_2,r_3\right)$ even though we call  the vector $\overrightarrow{r}.$  Again, we’re following Landau.

We take a fixed, inertial (or lab) coordinate system labeled $\left(X,Y,Z\right)$ and in this system the rigid body’s center of mass, labeled $O$, is at $\overrightarrow{R}$.  We have a Cartesian set of axes fixed in the body, origin at the center of mass, and coordinates in this system,  vectors from $O$ to a point in the body denoted by $\overrightarrow{r}$, are labeled $\left(x,y,z\right)$ or $\left(x_1,x_2,x_3\right)$.

  A vector from the external inertial fixed origin to a point in the body is then $$\overrightarrow{R}+\overrightarrow{r}=\overrightarrow{\rho },$$ say, as shown in the figure.

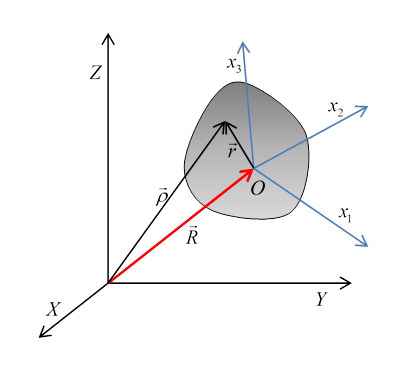
Suppose now that in infinitesimal time $dt$, the center of mass of the body moves $d\overrightarrow{R}$ and the body rotates through $d\overrightarrow{\varphi }$.  Then a particle at $\overrightarrow{r}$ as measured from the center of mass will move through $$d\overrightarrow{\rho }=d\overrightarrow{R}+d\overrightarrow{\varphi }\times \overrightarrow{r}$$ relative to the external inertial frame.

Therefore, the velocity of that particle in the fixed frame, writing the center of mass velocity and the angular velocity as $$d\overrightarrow{R}/dt=\overrightarrow{V},d\overrightarrow{\varphi }/dt=\overrightarrow{\Omega },$$  is

$$\overrightarrow{v}=\overrightarrow{V}+\overrightarrow{\Omega }\times \overrightarrow{r}.$$  Now, in deriving the above equation, we have not used the fact that the origin $O$ fixed in the body is at the center of mass. (That turns out to be useful shortly.)  What if instead we had taken some other origin $O^{\prime }$ fixed in the body? Would we find the angular velocity $\overrightarrow{{\Omega }^{\prime }}$ about $O^{\prime }$ to be the same as $\overrightarrow{\Omega }$? The answer turns out to be yes, but we need to prove it! Here's the proof:

 If the position of $O^{\prime }$ relative to $O$ is $\overrightarrow{a}$ (a vector fixed in the body and so moving with it) then the velocity $\overrightarrow{V^{\prime }}$ of $O^{\prime }$ is $$\overrightarrow{V^{\prime }}=\overrightarrow{V}+\overrightarrow{\Omega }\times \overrightarrow{a}$$ .

A particle at $\overrightarrow{r}$ relative to $O$ is at $\overrightarrow{r^{\prime }}=\overrightarrow{r}-\overrightarrow{a}$ relative to $O^{\prime }$ . 

Its velocity relative to the fixed external axes is $$\overrightarrow{v}=\overrightarrow{V^{\prime }}+\overrightarrow{{\Omega }^{\prime }}\times \overrightarrow{r^{\prime }},$$ this must of course equal $$\overrightarrow{V}+\overrightarrow{\Omega }\times \overrightarrow{r}=\overrightarrow{V}+\overrightarrow{\Omega }\times \overrightarrow{r^{\prime }}+\overrightarrow{\Omega }\times \overrightarrow{a}={\overrightarrow{V}}^{\prime }+\overrightarrow{\Omega }\times \overrightarrow{r^{\prime }}.$$ It follows that $\overrightarrow{{\Omega }^{\prime }}=\overrightarrow{\Omega }$.

This means that if we describe the motion of any particle in the body in terms of some origin fixed in the body, plus rotation about that origin, the angular velocity vector describing the body’s motion is the same irrespective of the origin we choose.  So we can, without ambiguity, talk about the angular velocity of the body.  

From now on, we’ll assume that the origin fixed in the body is at the center of mass.

The Inertia Tensor

 Regarding a rigid body as a system of individual particles, we find the kinetic energy

$$T={\displaystyle \sum _n\frac{1}{2}{m}_n{v}_n^2={\displaystyle \sum _n\frac{1}{2}{m}_n\left(\overrightarrow{V}+\overrightarrow{\Omega }\times {\overrightarrow{r}}_n\right)}}={\displaystyle \sum _n\frac{1}{2}{m}_n{V}^2+{\displaystyle \sum _n{m}_n\overrightarrow{V}\cdot \overrightarrow{\Omega }\times {\overrightarrow{r}}_n}}+{\displaystyle \sum _n\frac{1}{2}{m}_n{\left(\overrightarrow{\Omega }\times {\overrightarrow{r}}_n\right)}^2}.$$ The first term in the last line is$${\displaystyle \sum _n\frac{1}{2}{m}_n{V}^2=\frac{1}{2}M{V}^2,}$$ where $M$ is the total mass of the body.

  The second term is $${\displaystyle \sum _n{m}_n\overrightarrow{V}\cdot \overrightarrow{\Omega }\times {\overrightarrow{r}}_n}=\overrightarrow{V}\cdot \overrightarrow{\Omega }\times {\displaystyle \sum _n{m}_n{\overrightarrow{r}}_n}=0,$$ from the definition of the center of mass (our origin here)  ${\displaystyle \sum _n{m}_n{\overrightarrow{r}}_n}=0.$ 

 The third term can be rewritten: $${\displaystyle \sum _n\frac{1}{2}{m}_n{\left(\overrightarrow{\Omega }\times {\overrightarrow{r}}_n\right)}^2}={\displaystyle \sum _n\frac{1}{2}{m}_n\left[{\Omega }^2{r}_n^2-{\left(\overrightarrow{\Omega }\cdot {\overrightarrow{r}}_n\right)}^2\right]}.$$ Here we have used $$\left|\overrightarrow{\Omega }\times \overrightarrow{r}\right|=\Omega r\sin \theta ,\left|\overrightarrow{\Omega }\cdot \overrightarrow{r}\right|=\Omega r\cos \theta .$$

Alternatively, you could use the vector product identity $$\left(\overrightarrow{a}\times \overrightarrow{b}\right)\times \overrightarrow{c}=-\overrightarrow{a}\left(\overrightarrow{b}\cdot \overrightarrow{c}\right)+\overrightarrow{b}\left(\overrightarrow{a}\cdot \overrightarrow{c}\right)$$ together with $$\left(\overrightarrow{a}\times \overrightarrow{b}\right)\cdot \left(\overrightarrow{c}\times \overrightarrow{d}\right)=\left(\overrightarrow{a}\times \overrightarrow{b}\right)\times \overrightarrow{c}\cdot \overrightarrow{d}$$ to find $$\left(\overrightarrow{a}\times \overrightarrow{b}\right)\cdot \left(\overrightarrow{c}\times \overrightarrow{d}\right)=\left(\overrightarrow{a}\cdot \overrightarrow{c}\right)\left(\overrightarrow{b}\cdot \overrightarrow{d}\right)-\left(\overrightarrow{a}\cdot \overrightarrow{d}\right)\left(\overrightarrow{b}\cdot \overrightarrow{c}\right).$$ 

The bottom line is that the kinetic energy

$$T=\frac{1}{2}M{V}^2+{\displaystyle \sum _n\frac{1}{2}{m}_n\left[{\Omega }^2{r}_n^2-{\left(\overrightarrow{\Omega }\cdot {\overrightarrow{r}}_n\right)}^2\right]}=T_{\text{tr}}+T_{\text{rot}},$$ a translational kinetic energy plus a rotational kinetic energy.

Warning about notation:  at this point, things get a bit messy.  The reason is that to make further progress in dealing with the rotational kinetic energy, we need to write it in terms of the individual components of the $n$ particle position vectors ${\overrightarrow{r}}_n$ .  Following Landau and others, we’ll write these components in two different ways:

$${\overrightarrow{r}}_n=\left(x_n,y_n,z_n\right)\equiv \left(x_{n1},x_{n2},x_{n3}\right).$$ The $x,y,z$ notation is helpful in giving a clearer picture of rotational energy, but the $x_{ni}$ notation is essential in handling the math, as will become evident.

Landau’s solution to the too many suffixes for clarity problem is to omit the suffix $n$ labeling the individual particles, I prefer to keep it in.

Double Suffix Summation Notation:  to cut down on the number of ${\displaystyle \sum }$ ’s in expressions, we’ll follow Landau and others in using Einstein’s rule that if a suffix like $i,j,k$ appears twice in a product, it is to be summed over the values 1,2,3.  It’s called a “dummy suffix” because it doesn’t matter what you label it, as long as it appears twice.  For example, the inner product of two vectors $\overrightarrow{A}\cdot \overrightarrow{B}={\displaystyle \sum _{i=1}^3{A}_i{B}_i}$ can be written as $A_i{B}_i$ or equally as $A_k{B}_k$. Furthermore, ${\Omega }_i^2$ means ${\Omega }_1^2+{\Omega }_2^2+{\Omega }_3^2={\Omega }^2$.

 But do not use Greek letters for dummy suffixes in this context: the standard is that they are used in relativistic equations to signify sums over the four dimensions of space time, Latin letters for sums over the three spatial dimensions, as we are doing here.

The rotational kinetic energy is then

$$\begin{array}{c}{T}_{\text{rot}}=\frac{1}{2}{\displaystyle \sum _n{m}_n\left({\Omega }_i^2{x}_{ni}^2-{\Omega }_i{x}_{ni}{\Omega }_k{x}_{nk}\right)}\\ =\frac{1}{2}{\displaystyle \sum _n{m}_n\left({\Omega }_i{\Omega }_k{\delta }_{ik}{x}_{nl}^2-{\Omega }_i{\Omega }_k{x}_{ni}{x}_{nk}\right)}\\ =\frac{1}{2}{\Omega }_i{\Omega }_k{\displaystyle \sum _n{m}_n\left({\delta }_{ik}{x}_{nl}^2-x_{ni}{x}_{nk}\right)}.\end{array}$$

Warning:  That first line is a bit confusing:  copying Landau, I’ve written ${\Omega }_i^2{x}_{ni}^2$, you might think that’s ${\Omega }_1^2{x}_{n1}^2+{\Omega }_2^2{x}_{n2}^2+{\Omega }_3^2{x}_{n3}^2$, but a glance at the previous equation (and the second line of this equation) makes clear it’s actually ${\Omega }^2{r}^2$. Landau should have written ${\Omega }_i^2{x}_{nl}^2$.  Actually I’m not even keen on ${\Omega }_i^2$ implying a double summation.  Standard use in relativity, for example, is that both of the two suffixes be explicit for summation to be implied.  In GR one would write ${\Omega }_i{\Omega }_i$.   (Well, actually ${\Omega }_i{\Omega }^i$ , but that’s another story.)

Anyway, moving on, we introduce the inertia tensor

$$I_{ik}={\displaystyle \sum _n{m}_n\left(x_{nl}^2{\delta }_{ik}-x_{ni}{x}_{nk}\right)}$$

In terms of which the kinetic energy of the moving, rotating rigid body is

$$T=\frac{1}{2}M{V}^2+\frac{1}{2}{I}_{ik}{\Omega }_i{\Omega }_k.$$

As usual, the Lagrangian $L=T-V$ where the potential energy $V$ is a function of six variables in general, the center of mass location and the orientation of the body relative to the center of mass.

Landau writes the inertia tensor explicitly as:

$$I_{ik}=\left[\begin{array}{ccc}{\displaystyle \sum m\left(y^2+z^2\right)}& -{\displaystyle \sum mxy}& -{\displaystyle \sum mxz}\\ -{\displaystyle \sum mxy}& {\displaystyle \sum m\left(z^2+x^2\right)}& -{\displaystyle \sum myz}\\ -{\displaystyle \sum mxz}& -{\displaystyle \sum myz}& {\displaystyle \sum m\left(x^2+y^2\right)}\end{array}\right]$$

 

but you should bear in mind that $-{\displaystyle \sum mxz}$ means $-{\displaystyle \sum _n{m}_n{x}_n{z}_n}$.

Tensors 101

We see that the “inertia tensor” defined above as $$I_{ik}={\displaystyle \sum _n{m}_n\left(x_{nl}^2{\delta }_{ik}-x_{ni}{x}_{nk}\right)}$$ is a $3\times 3$ two-dimensional array of terms, called components, each of which is made up (for this particular tensor) of products of vector components. 

Obviously, if we had chosen a different set of Cartesian axes from the same origin $O$ the vector components would be different:  we know how a vector transforms under such a change of axes, $\left(x,y,z\right)\to \left(x^{\prime },y^{\prime },z^{\prime }\right)$ where

$$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ z^{\prime }\end{array}\right)=\left(\begin{array}{ccc}\cos \theta & \sin \theta & 0\\ -\sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right)\left(\begin{array}{c}x\\ y\\ z\end{array}\right).$$

This can be written more succinctly as

$${x^{\prime }}_i=R_{ij}{x}_j,\text{ or }{x}^{\prime }=Rx,$$

the bold font indicating a vector or matrix.

In fact, a transformation from any set of Cartesian axes to any other set having the same origin is a rotation about some axis.  This can easily be seen by first rotating so that the $x^{\prime }$ axis coincides with the $x$ axis, then rotating about that axis.  (Of course, both sets of axes must have the same handedness.)  We’ll discuss these rotation transformations in more detail later, for now we’ll just mention that the inverse of a rotation is given by the transpose matrix (check for the example above),

$$R^T=R^{-1},\text{or }{R}_{ji}=R_{ij}^{-1}$$

so if the column vector $${x^{\prime }}_i=R_{ij}{x}_j,\text{ or }{x}^{\prime }=Rx,$$ the row vector $${x^{\prime }}^T=x^T{R}^T=x^T{R}^{-1},$$ a.k.a. ${x^{\prime }}_i=R_{ij}{x}_j=x_j{R}_{ji}^T=x_j{R}_{ji}^{-1},$ and the length of the vector doesn’t change:

${x^{\prime }}_i{x^{\prime }}_i={x^{\prime }}^T{x}^{\prime }=x^T{R}^{T}Rx=x^T{R}^{-1}Rx=x^{T}x=x_i{x}_i.$

It might be worth spelling out explicitly here that the transpose of a square matrix (and almost all our matrices are square) is found by just swapping the rows and columns, or equivalently swapping elements which are the reflections of each other in the main diagonal, but the transpose of a vector, written as a column, has the same elements as a row, and the product of vectors follows the standard rules for matrix multiplication: $${\left(AB\right)}_{ij}=A_{ik}{B}_{kj},$$ with the dummy suffix $k$ summed over.

Thus, $${\left(\begin{array}{c}{a}_1\\ a_2\\ a_3\end{array}\right)}^T=\left(\begin{array}{ccc}{a}_1& a_2& a_3\end{array}\right),$$ and $$a^{T}a=\left(\begin{array}{ccc}{a}_1& a_2& a_3\end{array}\right)\left(\begin{array}{c}{a}_1\\ a_2\\ a_3\end{array}\right)=a_1^2+a_2^2+a_3^2,$$  but  $$a{a}^T=\left(\begin{array}{c}{a}_1\\ a_2\\ a_3\end{array}\right)\left(\begin{array}{ccc}{a}_1& a_2& a_3\end{array}\right)=\left(\begin{array}{ccc}{a}_1^2& a_1{a}_2& a_1{a}_3\\ a_1{a}_2& a_2^2& a_2{a}_3\\ a_1{a}_3& a_2{a}_3& a_3^2\end{array}\right).$$

This will perhaps remind you of the Hilbert space vectors in quantum mechanics: the transposed vector above is analogous to the bra, the initial column vector being the ket. One difference from quantum mechanics is that all our vectors here are real, if that were not the case it would be natural to add complex conjugation to the transposition, to give $a^{*}a={\left|a_1\right|}^2+{\left|a_2\right|}^2+{\left|a_3\right|}^2,$ the length squared of the vector.

The difference shown above between $a^{T}a$ and $a{a}^T$ is exactly parallel to the difference between $〈a\left|a\right.〉$ and $\left|a\right.〉\left.〈a\right|$ in quantum mechanics—the first is a number, the norm of the vector, the second is an operator, a projection into the state $\left|a\right.〉.$ 

Definition of a Tensor

We have a definite rule for how vector components transform under a change of basis: ${x^{\prime }}_i=R_{ij}{x}_j.$ What about the components of the inertia tensor $I_{ik}={\displaystyle \sum _n{m}_n\left(x_{nl}^2{\delta }_{ik}-x_{ni}{x}_{nk}\right)}$?

We’ll do it in two parts, and one particle at a time.  First, take that second term for one particle, it has the form $-m{x}_i{x}_k$.  But we already know how vector components transform, so this must go to

$$-m{x^{\prime }}_i{x^{\prime }}_k=R_{il}{R}_{jm}\left(-m{x}_l{x}_m\right).$$

The same rotation matrix $R_{ij}$ is applied to all the particles, so we can add over $n$.

In fact, the inertia tensor is made up of elements exactly of this form in all nine places, plus diagonal terms $m{r}_i^2$, obviously invariant under rotation. To make this clear, we write the inertia tensor:

$$\left[\begin{array}{ccc}{\displaystyle \sum m\left(y^2+z^2\right)}& -{\displaystyle \sum mxy}& -{\displaystyle \sum mxz}\\ -{\displaystyle \sum mxy}& {\displaystyle \sum m\left(z^2+x^2\right)}& -{\displaystyle \sum myz}\\ -{\displaystyle \sum mxz}& -{\displaystyle \sum myz}& {\displaystyle \sum m\left(x^2+y^2\right)}\end{array}\right]={\displaystyle \sum m\left(x^2+y^2+z^2\right)}1-\left[\begin{array}{ccc}{\displaystyle \sum m{x}^2}& {\displaystyle \sum mxy}& {\displaystyle \sum mxz}\\ {\displaystyle \sum mxy}& {\displaystyle \sum m{y}^2}& {\displaystyle \sum myz}\\ {\displaystyle \sum mxz}& {\displaystyle \sum myz}& {\displaystyle \sum m{z}^2}\end{array}\right]$$ 

where $1$ is the $3\times 3$ identity matrix.  (Not to be confused with $I$!)

Exercise: convince yourself that this is the same as $I={\displaystyle \sum m\left[\left(x^{T}x\right)1-x{x}^T\right]}.$ 

This transformation property is the definition of a two-suffix Cartesian three-dimensional tensor:  just as a vector in this space can be defined as an array of three components that are transformed under a change of basis by applying the rotation matrix, ${x^{\prime }}_i=R_{ij}{x}_j$, a tensor with two suffixes in the same space is a two-dimensional array of nine numbers that transform as

$${T^{\prime }}_{ij}=R_{il}{R}_{jm}{T}_{lm}.$$

Writing this in matrix notation, and keeping an eye on the indices, we see that with the standard definition of a matrix product, ${\left(AB\right)}_{ij}=A_{ik}{B}_{kj}$,

$$T^{\prime }=RT{R}^T=RT{R}^{-1}.$$

(The transformation property for our tensor followed immediately from that for a vector, since our tensor is constructed from vectors, but by definition the same rule applies to all Cartesian tensors, which are not always expressible in terms of vector components.)

Diagonalizing the Inertia Tensor

The inertial tensor has the form of a real symmetric matrix.  By an appropriate choice of axes $\left(x_1,x_2,x_3\right)$ any such tensor can be put in diagonal form, so that

$$T_{\text{rot}}=\frac{1}{2}\left(I_1{\Omega }_1^2+I_2{\Omega }_2^2+I_3{\Omega }_3^2\right).$$ These axes, with respect to which the inertia tensor is diagonal, are called the principal axes of inertia, the moments about them $I_1,I_2,I_3$  the principal moments of inertia.

If you’re already familiar with the routine for diagonalizing a real symmetric matrix, you can skip this review.

The diagonalization of the tensor/matrix proceeds as follows.

First, find the eigenvalues ${\lambda }_i$ and corresponding eigenvectors $e_i$ of the inertial tensor $I$ :

$$I{e}_i={\lambda }_i{e}_i\text{(}i=1,2,3,\text{ not summed)}$$

(The ${\lambda }_i$ turn out to be the principal moments $I_i$, but we’ll leave them as ${\lambda }_i$ for now, we need first to establish that they’re real.)

Now since $I$ is real and symmetric, $I^T=I$, the eigenvalues are real. To prove this, take the equation for $e_1$ above and premultiply by the row vector $e_1^{\ast T}$, the complex conjugate transpose:              

$$e_1^{*T}I{e}_1={\lambda }_1{e}_1^{*T}{e}_1\text{. }$$

The left hand side is a real number:  this can be established by taking its complex conjugate. The fact that the tensor is real and symmetric is crucial!

$${\left(e_{1i}^{\ast }{I}_{ij}{e}_{1j}\right)}^{\ast }=e_{1i}{I}_{ij}^{\ast }{e}_{1j}^{\ast }=e_{1i}{I}_{ji}{e}_{1j}^{\ast }=e_{1j}^{\ast }{I}_{ji}{e}_{1i},$$

And since these are dummy suffixes, we can swap the $i$ ’s and $j$ ’s to establish that this number is identical to its complex conjugate, hence it’s real.  Clearly, $e_1^{*T}{e}_1$ is real and positive, so the eigenvalues are real.

(Note: a real symmetric matrix does not necessarily have positive roots: for example $\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)$.)

Taking the eigenvalues to be distinct (the degenerate case is easy to deal with) the eigenvectors are orthogonal, by the standard proof, for this matrix left eigenvectors (rows) have the same eigenvalues as their transpose, so

$e_2^{T}I{e}_1={\lambda }_2{e}_2^T{e}_1={\lambda }_1{e}_2^T{e}_1,$

and $e_2^T{e}_1=0$. 

The diagonalizing matrix is made up of these eigenvectors (assumed normalized):

$$R=\left(\begin{array}{c}{e}_1^T\\ e_2^T\\ e_3^T\end{array}\right),$$

a column of row vectors. 

To check that this is indeed a rotation vector, from one orthogonal set of axes to another, notice first that its transpose $R^T=\left(\begin{array}{ccc}{e}_1& e_2& e_3\end{array}\right)$ is its inverse (as required for a rotation), since the eigenvectors form an orthonormal set.

Now apply this $R$ to an arbitrary vector:

$$x^{\prime }=Rx=\left(\begin{array}{c}{e}_1^T\\ e_2^T\\ e_3^T\end{array}\right)x=\left(\begin{array}{c}{e}_1^{T}x\\ e_2^{T}x\\ e_3^{T}x\end{array}\right)$$.

In vector language, these elements are just ${\overrightarrow{e}}_1\cdot \overrightarrow{x}$, etc., so ${x^{\prime }}_1={\overrightarrow{e}}_1\cdot \overrightarrow{x}$, the primed components are just the components of $\overrightarrow{x}$ along the eigenvector axes, so the operator $R$ gives the vector components relative to these axes, meaning it has rotated the coordinate system to one with the principal axes of the body are now the $x_1,x_2,x_3$ axes.

We can confirm this by applying the rotation to the inertia tensor itself:

$$I^{\prime }=RT{R}^T=\left(\begin{array}{c}{e}_1^T\\ e_2^T\\ e_3^T\end{array}\right)I\left(\begin{array}{ccc}{e}_1& e_2& e_3\end{array}\right)=\left(\begin{array}{c}{e}_1^T\\ e_2^T\\ e_3^T\end{array}\right)\left(\begin{array}{ccc}{\lambda }_1{e}_1& {\lambda }_2{e}_2& {\lambda }_3{e}_3\end{array}\right)=\left(\begin{array}{ccc}{\lambda }_1& 0& 0\\ 0& {\lambda }_2& 0\\ 0& 0& {\lambda }_3\end{array}\right).$$

Let’s examine the contribution of one particle to the inertia tensor:

                                                                            $I_1=m\left[\left(x^{T}x\right)1-x{x}^T\right]$

Note that $x$ here represents the column vector of the particle coordinates, in other words, it’s just $\overrightarrow{r}$! And, watch out for the inertia tensor $I$ and the unit tensor $1$. 

They transform as $x^{\prime }=Rx$, note that this agrees with $I^{\prime }=RI{R}^T$.  Since under rotation the length of a vector is invariant, ${x^{\prime }}^T{x}^{\prime }=x^{T}x$, and $Rx{x}^T{R}^T=x^{\prime }{x^{\prime }}^T$ it is evident that in the rotated frame (the eigenvector frame) the single particle contributes to the diagonal elements $$m\left[\left(x_2^2+x_3^2\right),\left(x_3^2+x_1^2\right),\left(x_1^2+x_2^2\right)\right]$$. We’ve dropped the primes, since we’ll be working in this natural frame from now on.

Principal Axes Form of Moment of Inertia Tensor

We already know that the transformed matrix is diagonal, so its form has to be

$${\displaystyle \sum _n{m}_n\left(\begin{array}{ccc}{x}_{n2}^2+x_{n3}^2& 0& 0\\ 0& x_{n3}^2+x_{n1}^2& 0\\ 0& 0& x_{n1}^2+x_{n2}^2\end{array}\right)}=\left(\begin{array}{ccc}{I}_1& 0& 0\\ 0& I_2& 0\\ 0& 0& I_3\end{array}\right).$$

The moments of inertia, the diagonal elements, are of course all positive.  Note that no one of them can exceed the sum of the other two, although it can be equal in the (idealized) case of a two-dimensional object.  For that case, taking it to lie in the $\left(x,y\right)$ plane, $$I_z={\displaystyle \sum _n\left(x_n^2+y_n^2\right)}=I_x+I_y.$$.

Relating Angular Momentum to Angular Velocity

It’s easy to check that the angular momentum vector is

$$L_i=I_{ij}{\Omega }_j,$$since

$L={\displaystyle \sum {\overrightarrow{r}}_n}\times m_n{\overrightarrow{v}}_n={\displaystyle \sum m_n{\overrightarrow{r}}_n}\times \left(\overrightarrow{\Omega }\times {\overrightarrow{r}}_n\right)=\overrightarrow{\Omega }{\displaystyle \sum m_n{r}_n^2}-{\displaystyle \sum m_n{\overrightarrow{r}}_n}\left(\overrightarrow{\Omega }\cdot {\overrightarrow{r}}_n\right)=I\overrightarrow{\Omega }.$

Exercise:  verify this by putting in all the suffixes.

Symmetries, Other Axes, the Parallel Axis Theorem

If a body has an axis of symmetry, the center of mass must be on that axis, and it is a principal axis of inertia. To prove the center of mass statement, note that the body is made up of pairs of equal mass particles on opposite sides of the axis, each pair having its center of mass on the axis, and the body’s center of mass is that of all these pairs centers of mass, all of which are on the axis.  

Taking this axis to be the $x$ axis, symmetry means that for each particle at $\left(x,y,z\right)$ there is one of equal mass at $\left(x,-y,-z\right)$, so the off-diagonal terms in the $x$ row and column, $-{\displaystyle \sum mxy,}-{\displaystyle \sum mxz}$ all add up to zero, meaning this is indeed a principal axis.

The moment of inertia about an arbitrary axis through the center of mass, in the direction of the unit vector $\widehat{\overrightarrow{b}},$ is

${\displaystyle \sum m\left({\overrightarrow{r}}^2-{\left(\overrightarrow{r}\cdot \widehat{\overrightarrow{b}}\right)}^2\right)}={\widehat{\overrightarrow{b}}}^{T}I\widehat{\overrightarrow{b}}=b_x^2{I}_x+b_y^2{I}_y+b_z^2{I}_z$.

The inertia tensor about some origin $O^{\prime }$ located at position $a$ relative to the center of mass is easily found to be

$${I^{\prime }}_{ik}=I_{ik}+M\left(a^2{\delta }_{ik}-a_i{a}_k\right).$$

In particular, we have the parallel axis theorem: the moment of inertia about any axis through some point $O^{\prime }$ equals that about the parallel axis through the center of mass $O$ plus $M{a}_{\perp }^2$, where $a_{\perp }$ is the perpendicular distance between the axes.

Exercise: check this!

 previous  home  next  PDF