previous  home  next  PDF

26. Euler’s Angles

Michael Fowler

Introduction

So far, our analysis of rotational motion has been of essentially one dimensional, or more precisely one angular parameter, motion: rotating about an axis, rolling, precessing and so on. But this leaves out many interesting phenomena, for example the wobbling of a slowing down top, nutation, and so on. We need a well-defined set of parameters for the orientation of a rigid body in space to make further progress in analyzing the dynamics.

The standard set is Euler’s Angles. What you see as you watch a child’s top beginning to wobble as it slows down is the direction of the axis$—$this is given by the first two of Euler’s angles: $\theta ,\varphi$ the usual spherical coordinates, the angle $\theta$ from the vertical direction and the azimuthal angle $\varphi$ about that vertical axis.  Euler’s third angle, $\psi ,$ specifies the orientation of the top about its own axis, completing the description of the precise positioning of the top. To describe the motion of the wobbling top as we see it, we evidently need to cast the equations of motion in terms of these angles.

Definition

The rotational motion of a rigid body is completely defined by tracking the set of principal axes $\left(x_1,x_2,x_3\right)$, with origin at the center of mass, as they turn relative to a set of fixed axes $\left(X,Y,Z\right).$ The principal axes can be completely defined relative to the fixed set by three angles: the two angles $\left(\theta ,\varphi \right)$ fix the direction of $x_3,$ but that leaves the pair $x_1,x_2$ free to turn in the plane perpendicular to $x_3,$ the angle $\psi$ fixes their orientation. 

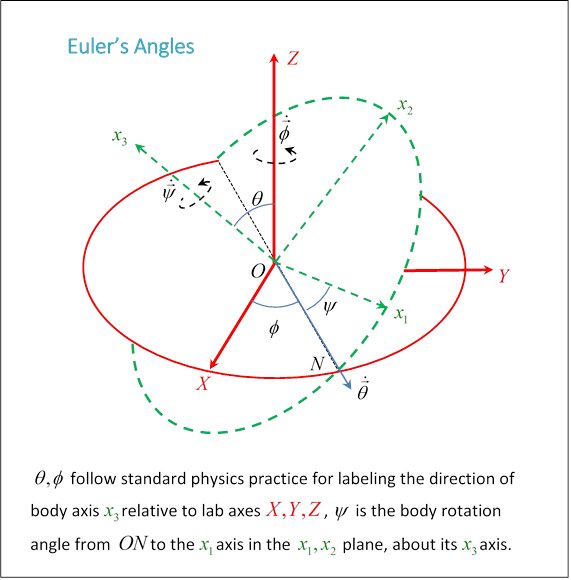
To see these angles, start with the fixed axes, draw a circle centered at the origin in the horizontal $X,Y$ plane. Now draw a circle of the same size, also centered at the same origin, but in the principal axes $x_1,x_2$ plane.  Landau calls the line of intersection of these circles (or discs) the line of nodes. It goes through the common origin, and is a diameter of both circles.

The angle between these two planes, which is also the angle between $Z,x_3$ (since they’re the perpendiculars to the planes) is labeled $\theta .$ 

The angle between this line of nodes and the $X$ axis is $\varphi .$ It should be clear that $\theta ,\varphi$ together fix the direction of $x_3,$ then the other axes are fixed by giving $\psi ,$ the angle between $x_1$ and the line of nodes $ON.$ The direction of measurement of $\varphi ,\psi$ around $Z,x_3$ are given by the right-hand or corkscrew rule.

Angular Velocity and Energy in Terms of Euler’s Angles

Since the position is uniquely defined by Euler’s angles, angular velocity is expressible in terms of these angles and their derivatives.  

The strategy here is to find the angular velocity components along the body axes $x_1,x_2,x_3$ of $\dot{\theta },\dot{\varphi },\dot{\psi }$ in turn.  Once we have the angular velocity components along the principal axes, the kinetic energy is easy.

(You might be thinking: wait a minute, aren't the axes embedded in the body? Don't they turn with it?  How can you talk about rotation about these axes? Good point: what we're doing here is finding the components of angular velocity about a set of axes fixed in space, not the body, but momentarily coinciding with the principal axes of the body.)

From the diagram, $\dot{\theta }$ is along the line $ON,$ and therefore in the $x_1,x_2$ plane: notice it is at an angle $-\psi$ with respect to $x_1.$ Its components are therefore $\dot{\overrightarrow{\theta }}=\left(\dot{\theta }\cos \psi ,-\dot{\theta }\sin \psi ,0\right).$ 

Now $\dot{\varphi }$ is about the $Z$ axis. The principal axis $x_3$ is at angle $\theta$ to the $Z$ axis, so $\dot{\overrightarrow{\varphi }}$ has component $\dot{\varphi }\cos \theta$ about $x_3,$ and $\dot{\varphi }\sin \theta$ in the $x_1,x_2$ plane, that latter component along a line perpendicular to $ON$, and therefore at angle $-\psi$ from the $x_2$ axis. Hence $\dot{\overrightarrow{\varphi }}=\left(\dot{\varphi }\sin \theta \sin \psi ,\dot{\varphi }\sin \theta \cos \psi ,\dot{\varphi }\cos \theta \right).$ 

The angular velocity $\dot{\psi }$ is already along a principal axis, $x_3.$ 

To summarize, the Euler angle angular velocities (components along the body’s principal axes) are:

$$\begin{array}{l}\dot{\overrightarrow{\theta }}=\left(\dot{\theta }\cos \psi ,-\dot{\theta }\sin \psi ,0\right),\\ \dot{\overrightarrow{\varphi }}=\left(\dot{\varphi }\sin \theta \sin \psi ,\dot{\varphi }\sin \theta \cos \psi ,\dot{\varphi }\cos \theta \right),\\ \dot{\overrightarrow{\psi }}=\left(\begin{array}{ccc}0,& 0,& \dot{\psi }\end{array}\right),\end{array}$$ from which, the angular velocity components along those in-body axes $x_1,x_2,x_3$ are:

$$\begin{array}{l}{\Omega }_1=\dot{\varphi }\sin \theta \sin \psi +\dot{\theta }\cos \psi ,\\ {\Omega }_2=\dot{\varphi }\sin \theta \cos \psi -\dot{\theta }\sin \psi ,\\ {\Omega }_3=\dot{\varphi }\cos \theta +\dot{\psi }.\end{array}$$ For a symmetric top, meaning $I_1=I_2\ne I_3,$ the rotational kinetic energy is therefore

$$T_{\text{rot}}=\frac{1}{2}{I}_1\left({\Omega }_1^2+{\Omega }_2^2\right)+\frac{1}{2}{I}_3{\Omega }_3^2=\frac{1}{2}{I}_1\left({\dot{\varphi }}^2{\sin }^2\theta +{\dot{\theta }}^2\right)+\frac{1}{2}{I}_3{\left(\dot{\varphi }\cos \theta +\dot{\psi }\right)}^2.$$ For this symmetrical case, as Landau points out, we could have taken the $x_1$ axis momentarily along the line of nodes $ON,$ giving

$\overrightarrow{\Omega }=\left(\dot{\theta },\dot{\varphi }\sin \theta ,\dot{\varphi }\cos \theta +\dot{\psi }\right).$

Free Motion of a Symmetrical Top

As a warm up in using Euler’s angles, we’ll redo the free symmetric top covered in the last lecture. With no external torques acting the top will have constant angular momentum $\overrightarrow{L}.$ 

We’ll take $\overrightarrow{L}$ in the fixed $Z$ direction. The axis of the top is along $x_3.$ 

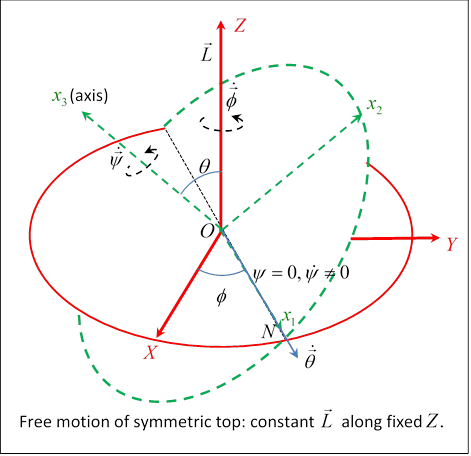
 Taking the $x_1$ axis along the line of nodes $ON$ (see figure below) at the instant considered, the constant angular momentum $\begin{array}{c}\overrightarrow{L}=\left(I_1{\Omega }_1,I_1{\Omega }_2,I_3{\Omega }_3\right)\\ =\left(I_1\dot{\theta },I_1\dot{\varphi }\sin \theta ,I_3\left(\dot{\varphi }\cos \theta +\dot{\psi }\right)\right).\end{array}$

Remember, this new $x_1$ axis (see diagram!) is perpendicular to the $Z$ axis we’ve taken $\overrightarrow{L}$ along, so $L_1=I_1\dot{\theta }=0,$ and $\theta$ is constant, meaning that the principal axis $x_3$ describes a cone around the constant angular momentum vector $\overrightarrow{L}.$ The rate of precession follows from the constancy of $L_2=I_1\dot{\varphi }\sin \theta .$  Writing the absolute magnitude of the angular momentum as $L,$ $L_2=L\sin \theta ,$ (remember $L$ is in the $Z$ direction, and $x_1$ is momentarily along $ON$ )  so the rate of precession $\dot{\varphi }=L/I_1.$ Finally, the component of $\overrightarrow{L}$ along the $x_3$ axis of symmetry of the top is $L\cos \theta =I_3{\Omega }_3,$ so the top’s spin along its own axis is ${\Omega }_3=\left(L/I_3\right)\cos \theta .$ 

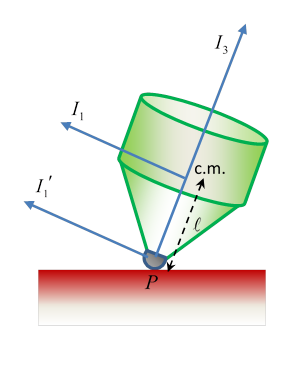
Motion of Symmetrical Top around a Fixed Base with Gravity:  Nutation

Denoting the distance of the center of mass from the fixed bottom point $P$ as $\ell$ (along the axis) the moment of inertia about a line perpendicular to the axis at the base point is

${I^{\prime }}_1=I_1+M{\ell }^2.$

( $I_1$ being usual center of mass moment.)

The Lagrangian is ( $P$ being the origin, $I_3$ in direction $\theta ,\varphi$ ) $$L=\frac{1}{2}{I^{\prime }}_1\left({\dot{\varphi }}^2{\sin }^2\theta +{\dot{\theta }}^2\right)+\frac{1}{2}{I}_3{\left(\dot{\varphi }\cos \theta +\dot{\psi }\right)}^2-Mg\ell \cos \theta .$$ Notice that the coordinates $\psi ,\varphi$ do not appear explicitly, so there are two constants of motion:

$$\begin{array}{l}{p}_{\psi }=\partial L/\partial \dot{\psi }=I_3\left(\dot{\varphi }\cos \theta +\dot{\psi }\right)=L_3,\\ p_{\varphi }=\partial L/\partial \dot{\varphi }=\left({I^{\prime }}_1{\sin }^2\theta +I_3{\cos }^2\theta \right)\dot{\varphi }+I_3\dot{\psi }\cos \theta =L_Z.\end{array}$$ That is, the angular momentum about $x_3$ is conserved, because the two forces acting on the top, the gravitational pull at the center of mass and the floor reaction at the bottom point, both act along lines intersecting the axis, so never have torque about $x_3.$ The angular momentum about $Z$ is conserved because the gravitational torque acts perpendicular to this line.

We have two linear equations in $\dot{\psi },\dot{\varphi }$ with coefficients depending on $\theta$ and the two constants of motion $L_3,L_Z.$ The solution is straightforward, giving

$$\dot{\varphi }=\frac{L_Z-L_3\cos \theta }{{I^{\prime }}_1{\sin }^2\theta },\dot{\psi }=\frac{L_3}{I_3}-\cos \theta \left(\frac{L_Z-L_3\cos \theta }{{I^{\prime }}_1{\sin }^2\theta }\right).$$ The (conserved) energy

$$\begin{array}{c}E=\frac{1}{2}{I^{\prime }}_1\left({\Omega }_1^2+{\Omega }_2^2\right)+\frac{1}{2}{I}_3{\Omega }_3^2+Mg\ell \cos \theta \\ =\frac{1}{2}{I^{\prime }}_1\left({\dot{\varphi }}^2{\sin }^2\theta +{\dot{\theta }}^2\right)+\frac{1}{2}{I}_3{\left(\dot{\varphi }\cos \theta +\dot{\psi }\right)}^2+Mg\ell \cos \theta .\end{array}$$ Using the constants of motion to express $\dot{\psi },\dot{\varphi }$ in terms of $\theta$ and the constants $L_Z,L_3$ , then subtracting a $\theta$ independent term to reduce clutter, $$E^{\prime }=E-Mg\ell -\left(L_3^2/2I_3\right),$$ we have

$$E^{\prime }=\frac{1}{2}{I^{\prime }}_1{\dot{\theta }}^2+V_{\text{eff}}\left(\theta \right),V_{\text{eff}}\left(\theta \right)=\frac{{\left(L_Z-L_3\cos \theta \right)}^2}{2{I^{\prime }}_1{\sin }^2\theta }-Mg\ell \left(1-\cos \theta \right).$$ The range of motion in $\theta$ is given by $E^{\prime }>V_{\text{eff}}\left(\theta \right).$ For $L_3\ne L_Z,$ $V_{\text{eff}}\left(\theta \right)$ goes to infinity at $\theta =0,\pi$. It has a single minimum between these points.  (This isn’t completely obvious$—$one way to see it is to change variable to $u=\cos \theta$, following Goldstein. Multiplying throughout by ${\sin }^2\theta$, and writing ${\dot{\theta }}^2{\sin }^2\theta ={\dot{u}}^2$ gives a one dimensional particle in a potential problem, and the potential is a cubic in $u.$ Of course some roots of  $E^{\prime }=V_{\text{eff}}\left(\theta \right)$ could be in the unphysical region $\left|u\right|>1.$ In any case, there are at most three roots, so since the potential is positive and infinite at $\theta =0,\pi ,$ it has at most two roots in the physical range.)

From the one-dimensional particle in a potential analogy, it’s clear that $\theta$ oscillates between these two points ${\theta }_1$ and ${\theta }_2.$ This oscillation is called nutation.  Now $\dot{\varphi }=\left(L_Z-L_3\cos \theta \right)/{I^{\prime }}_1{\sin }^2\theta$ could change sign during this oscillation, depending on whether or not the angle ${\cos }^{-1}\left(L_Z/L_3\right)$ is in the range. Visualizing the path of the top center point on a spherical surface centered at the fixed point, as it goes around it oscillates up and down, but if there is this sign change, it will “loop the loop”, going backwards on the top part of the loop.

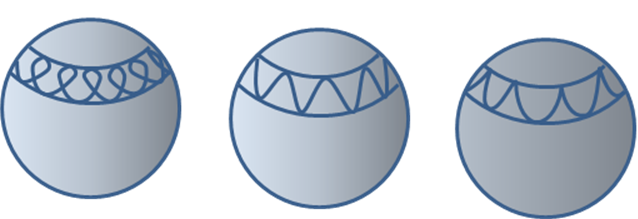
Steady Precession

Under what conditions will a top, spinning under gravity, precess at a steady rate?  The constancy of $L_3,L_Z$ mean that ${\Omega }_3=\dot{\varphi }\cos \theta +\dot{\psi },\text{ and }{\Omega }_{\text{pr}}=\dot{\varphi }$ are constants.

The $\theta$ Lagrange equation is

$I_1{}^{\prime }\ddot{\theta }=I_1{}^{\prime }{\dot{\varphi }}^2\sin \theta \cos \theta -I_3\left(\dot{\varphi }\cos \theta +\dot{\psi }\right)\dot{\varphi }\sin \theta +Mg\ell \sin \theta$

For constant $\theta ,$ $\ddot{\theta }=0,$ so, with ${\Omega }_3=\dot{\varphi }\cos \theta +\dot{\psi },\text{ and }{\Omega }_{\text{pr}}=\dot{\varphi },$  

$I_1{}^{\prime }{\Omega }_{pr}^2\cos \theta -I_3{\Omega }_3{\Omega }_{pr}+Mg\ell =0.$

Since this is a quadratic equation for the precession rate, there are two solutions in general: on staring at a precessing top, this is a bit surprising!  We know that for the top, when it’s precessing nicely, the spin rate ${\Omega }_3$ far exceeds the precession rate ${\Omega }_{pr}.$  Assuming $I_1{}^{\prime },I_3$ to be of similar size, this means the first term in the quadratic is much smaller than the second. If we just drop the first term, we get the precession rate

$${\Omega }_{\text{precess (slow)}}=\frac{Mg\ell }{I_3{\Omega }_3},\left({\Omega }_3\gg {\Omega }_{\text{precess}}\right).$$ Note that this is independent of angle$—$the torque varies as $\sin \theta ,$ but so does the horizontal component of the angular momentum, which is what’s changing.

This is the familiar solution for a child’s fast-spinning top precessing slowly.  But this is a quadratic equation, there’s another possibility: in this large ${\Omega }_3$ limit, this other possibility is that ${\Omega }_{pr}$ is itself of order ${\Omega }_3$, so now in the equation the last term, the gravitational one, is negligible, and

${\Omega }_{\text{precess (fast)}}\cong I_3{\Omega }_3/I_1{}^{\prime }\cos \theta .$

This is just the nutation of a free top!  In fact, of course, both of these are approximate solutions, only exact in the limit of infinite spin (where one goes to zero, the other to infinity), and a more precise treatment will give corrections to each arising from the other.  Landau indicates the leading order gravitational correction to the free body nutation mode.

Stability of Top Spinning about Vertical Axis

(from Landau) For $\theta =\dot{\theta }=0,L_3=L_Z,E^{\prime }=0.$ Near $\theta =0,$ 

$$\begin{array}{c}{V}_{\text{effective}}\left(\theta \right)=\frac{{\left(L_Z-L_3\cos \theta \right)}^2}{2{I^{\prime }}_1{\sin }^2\theta }-Mg\ell \left(1-\cos \theta \right)\\ \cong \frac{L_3^2{\left(\frac{1}{2}{\theta }^2\right)}^2}{2{I^{\prime }}_1{\theta }^2}-\frac{1}{2}Mg\ell {\theta }^2\\ =\left(L_3^2/8I_1{}^{\prime }-\frac{1}{2}Mg\ell \right){\theta }^2\end{array}$$ The vertical position is stable against small oscillations provided  $L_3^2>4{I^{\prime }}_{1}Mg\ell ,$ or ${\Omega }_3^2>4{I^{\prime }}_{1}Mg\ell /I_3^2.$

Exercise: suppose you set the top vertical, but spinning at less than ${\Omega }_{3\text{ crit}}$, the value at which it is just stable.  It will fall away, but bounce back, and so on. Show the maximum angle it reaches is given by $\cos \left(\theta /2\right)={\Omega }_3/{\Omega }_{3\text{ crit}}.$ 

 previous  home  next  PDF