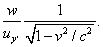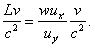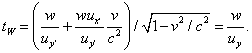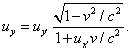Adding Velocities: A Walk on the Train
The Formula
If I walk from the back to the front of a train at 3 m.p.h., and the train is traveling at 60 m.p.h., then common sense tells me that my speed relative to the ground is 63 m.p.h. As we have seen, this obvious truth, the simple addition of velocities, follows from the Galilean transformations. Unfortunately, it can’t be quite right for high speeds! We know that for a flash of light going from the back of the train to the front, the speed of the light relative to the ground is exactly the same as its speed relative to the train, not 60 m.p.h. different. Hence it is necessary to do a careful analysis of a fairly speedy person moving from the back of the train to the front as viewed from the ground, to see how velocities really add.
We consider our standard train of
length L moving down the track at steady speed v, and equipped
with synchronized clocks at the back and the front. The walker sets off from the back of the
train when that clock reads zero.
Assuming a steady walking speed of u meters per second (relative
to the train, of course), the walker will see the front clock to read L/u
seconds on arrival there.
How does this look from the ground? Let’s assume that at the instant the walker began to walk from the clock at the back of the train, the back of the train was passing the ground observer’s clock, and both these clocks (one on the train and one on the ground) read zero. The ground observer sees the walker reach the clock at the front of the train at the instant that clock reads L/u (this is in agreement with what is observed on the train—two simultaneous events at the same place are simultaneous to all observers), but at this same instant, the ground observer says the train’s back clock, where the walker began, reads L/u + Lv/c2. (This follows from our previously established result that two clocks synchronized in one frame, in which they are L apart, will be out of synchronization in a frame in which they are moving at v along the line joining them by a time Lv/c2.)
Now, how much time elapses as measured by the ground observer’s clock during the walk? At the instant the walk began, the ground observer saw the clock at the back of the train (which was right next to him) to read zero. At the instant the walk ended, the ground observer would say that clock read L/u + Lv/c2, from the paragraph above. But the ground observer would see that clock to be running slow, by the usual time dilation factor: so he would measure the time of the walk on his own clock to be:

How far does the walker move as viewed from the ground? In the time tW, the train travels a distance vtW, so the walker moves this distance plus the length of the train. Remember that the train is contracted as viewed from the ground! It follows that the distance covered relative to the ground during the walk is:

The walker’s speed relative to the ground is simply dW/tW, easily found from the above expressions:
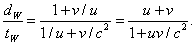
This is the appropriate formula for adding velocities. Note that it gives the correct answer, u + v, in the low velocity limit, and also if u or v equals c, the sum of the velocities is c.
Exercise 1: The direct
derivation given above is really equivalent to a rederivation of the Lorentz
equations. The equation describing the walker's path on the train is just x'
= ut'. Substitute this in the Lorentz equations and prove it leads to a
path relative to the ground given by x = wt, with w given by the
velocity addition formula.
Exercise 2: Suppose a spaceship is equipped with a series of one-shot rockets, each of which can accelerate the ship to c/2 from rest. It uses one rocket to leave the solar system (ignore gravity here) and is then traveling at c/2 (relative to us) in deep space. It now fires its second rocket, keeping the same direction. Find how fast it is moving relative to us. It now fires the third rocket, keeping the same direction. Find its new speed. Can you draw any general conclusions from your results?