Damped Driven Oscillator Near Resonance
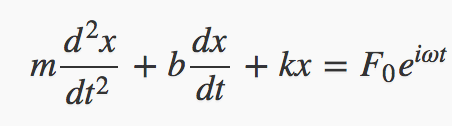
This applet is a first look at the behavior of a damped driven oscillator near resonance, described by the differential equation above, the full mathematical details can be found in my lecture. We’ve set initial values of natural oscillation frequency omega_0 = 1, and a driving frequency 1.1, and we've set the damping zero for now. Observe the wavepackets (beats) generated. Check out the walk-through to learn more about damped driven oscillators near resonance using this applet.
Walk-Through
How do you think this will change for omega = 1.05? (Keeping the damping zero.)
Try it! (You can adjust the driving force to scale the curve.) Then try 1.025. How, exactly, has the pattern changed?
What happens at omega = 0.9? Check it out. How does this curve differ from the omega = 1.1 curve? Or does it?
Now do omega = 1, but now add damping b = 0.08.
Explore different values of damping, but adjust the driving force strength so the pattern is a reasonable size on the screen.
Show you can choose the initial position and velocity so that the oscillations initially decrease in magnitude.
Can that be done for driving at the resonant frequency? Check it out!
What curve do you expect if you put the spring constant k = 0?
What about k = 0 and F = 0? (Put b nonzero.) Try nonzero initial position, zero and nonzero initial velocities. Is that what you expect from looking at the equation?
Here's the relevant lecture.
Program by: Carter Hedinger