Galileo on Projectiles
Beginning on page 244 of Two New Sciences, Galileo gives his classic analysis of the motion of a projectile as a compound motion, made up of a horizontal motion which has steady speed in a fixed direction, and a vertical motion which is his "naturally accelerated motion" picking up velocity in the downward direction at a steady rate. Don't worry about the bits of Greek geometry mentioned near the beginning, I've left in one or two remarks to give the flavor, but cut out the main argument - we shall just take a parabola to be defined as y proportional to x2.
It is interesting to note the difficulties raised towards the end, and Galileo's rebuttals. It is noted that, when Galileo asserts that a frictionless ball on a truly flat plane with no air resistance would roll on forever, Simp points out that going far enough on a really flat plane would mean moving away from the earth, in other words, it would become "uphill". Galileo admits this effect exists, but just claims it is a negligible correction, even for projectiles going four miles, apparently the furthest anything had been shot at the time.
Galileo shows a modern scientific attitude in realizing that his results are not exact, but that that need not be important. The main thing is to be sure how large the errors are, and thus whether or not they matter for the task at hand. This is very different from the attitude of Greek geometers, who were only interested in precise results - yet Galileo's is the only way in which their work can be used to understand the real physical world.
FOURTH DAY
SALVIATI. Once more, Simplicio is here on time; so let us without delay take up the question of motion. The text of our Author follows:
THE MOTION OF PROJECTILES
In the preceding pages we have discussed the properties of uniform motion and of motion naturally accelerated along planes of all inclinations. I now propose to set forth those properties which belong to a body whose motion is compounded of two other motions, namely, one uniform and one naturally accelerated; these properties, well worth knowing, I propose to demonstrate in a rigid manner. This is the kind of motion seen in a moving projectile; its origin I conceive to be as follows:
Imagine any particle projected along a horizontal plane without friction; then we know, from what has been more fully explained in the preceding pages, that this particle will move along this same plane with a motion which is uniform and perpetual, provided the plane has no limits. But if the plane is limited and elevated, then the moving particle, which we imagine to be a heavy one, will on passing over the edge of the plane acquire, in addition to its previous uniform and perpetual motion, a downward propensity due to its own weight; so that the resulting motion which I call projection is compounded of one which is uniform and horizontal and of another which is vertical and naturally accelerated. We now proceed to demonstrate some of its properties, the first of which is as follows:
THEOREM 1, PROPOSITION I
A projectile which is carried by a uniform horizontal motion compounded with a naturally accelerated vertical motion describes a path which is a semi-parabola.
SAGR. Here, Salviati, it will be necessary to stop a little while for my sake and, I believe, also for the benefit of Simplicio; for it so happens that I have not gone very far in my study of Apollonius and am merely aware of the fact that he treats of the parabola and other conic sections, without an understanding of which I hardly think one will be able to follow the proof of other propositions depending upon them. Since even in this first beautiful theorem the author finds it necessary to prove that the path of a projectile is a parabola, and since, as I imagine, we shall have to deal with only this kind of curves, it will be absolutely necessary to have a thorough acquaintance, if not with all the properties which Apollonius has demonstrated for these figures, at least with those which are needed for the present treatment.
(At this point, Galileo demonstrates his dexterity in traditional Greek geometry, to the consternation of Simplicio, and proves that if a cone is cut by a plane parallel to the side of the cone, the outline of the cut section is a parabola. You can look up the details in the book, if you're interested. We come in below at the very end of the proof, just to give you the flavor of the exchange. )
SIMP. Your demonstration proceeds too rapidly and, it seems to me, you keep on assuming that all of Euclid's theorems are as familiar and available to me as his first axioms, which is far from true. And now this fact which you spring upon us, that four times the rectangle ea. ad is less than the square of de because the two portions ea and ad of the line de are not equal brings me little composure of mind, but rather leaves me in suspense.
SALV. Indeed, all real mathematicians assume on the part of the reader perfect familiarity with at least the elements of Euclid.
(He goes on to prove the last point in the argument. The whole argument was to establish that a parabola, defined as a section of a cone, has the form y proportional to x2 . Of course, if we simply define a parabola by this equation, there's nothing to prove - except that we do have to establish, as discussed below, that the "compound" motion of a projectile means its path through space is in fact a parabola. )
We can now resume the text and see how he demonstrates his first proposition in which he shows that a body falling with a motion compounded of a uniform horizontal and a naturally accelerated one describes a semi-parabola.
Let us imagine an elevated horizontal line or plane ab along which a body moves with uniform speed from a to b. Suppose this plane to end abruptly at b; then at this point the body will, on account of its weight, acquire also a natural motion downwards along the perpendicular bn.
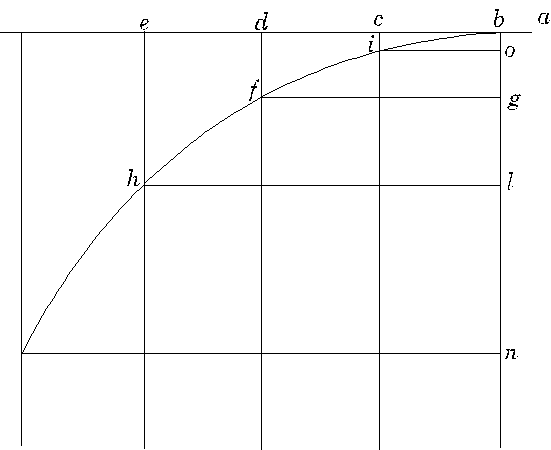
Draw the line be along the plane ba to represent the flow, or measure, of time; divide this line into a number of segments, bc, cd, de, representing equal intervals of time; from the points b, c, d, e, let fall lines which are parallel to the perpendicular bn. On the first of these lay off any distance ci, on the second a distance four times as long, df; on the third, one nine times as long, eh; and so on, in proportion to the squares of cb, db, eb, or, we may say, in the squared ratio of these same lines. Accordingly we see that while the body moves from b to c with uniform speed, it also falls perpendicularly through the distance ci, and at the end of the time-interval bc finds itself at the point i. In like manner at the end of the time-interval bd, which is the double of bc, the vertical fall will be four times the first distance ci; for it has been shown in a previous discussion that the distance traversed by a freely falling body varies as the square of the time; in like manner the space eh traversed during the time be will be nine times ci; thus it is evident that the distances eh, df, cl will be to one another as the squares of the lines be, bd, bc. Now from the points i, f, h draw the straight lines io, fg, hl parallel to be; these lines hl, fg, io are equal to eb, db and cb, respectively; so also are the lines bo, bg, bl respectively equal to ci, df, and eh. The square of hl is to that of fg as the line lb is to bg; and the square of fg is to that of io as gb is to bo; therefore the points i, f, h, lie on one and the same parabola. In like manner it may be shown that, if we take equal time-intervals of any size whatever, and if we imagine the particle to be carried by a similar compound motion, the positions of this particle, at the ends of these time-intervals, will lie on one and the same parabola. Q. E. D.
(Note that in the above, Galileo is using the horizontal intervals bc, cd, etc. , to denote time as well as distance. This is ok, since the horizontal motion is at steady speed, but is rather confusing!)
SAGR. One cannot deny that the argument is new, subtle and conclusive, resting as it does upon this hypothesis, namely, that the horizontal motion remains uniform, that the vertical motion continues to be accelerated downwards in proportion to the square of the time, and that such motions and velocities as these combine without altering, disturbing, or hindering each other, so that as the motion proceeds the path of the projectile does not change into a different curve: but this, in my opinion, is impossible. For the axis of the parabola along which we imagine the natural motion of a falling body to take place stands perpendicular to a horizontal surface and ends at the center of the earth; and since the parabola deviates more and more from its axis no projectile can ever reach the center of the earth or, if it does, as seems necessary, then the path of the projectile must transform itself into some other curve very different from the parabola.
SIMP. To these difficulties, I may add others. One of these is that we suppose the horizontal plane, which slopes neither up nor down, to be represented by a straight line as if each point on this line were equally distant from the center, which is not the case; for as one starts from the middle [of the line] and goes toward either end, he departs farther and farther from the center [of the earth] and is therefore constantly going uphill. Whence it follows that the motion cannot remain uniform through any distance whatever, but must continually diminish. Besides, I do not see how it is possible to avoid the resistance of the medium which must destroy the uniformity of the horizontal motion and change the law of acceleration of falling bodies. These various difficulties render it highly improbable that a result derived from such unreliable hypotheses should hold true in practice.
SALV. All these difficulties and objections which you urge are so well founded that it is impossible to remove them; and, as for me, I am ready to admit them all, which indeed I think our author would also do. I grant that these conclusions proved in the abstract will be different when applied in the concrete and will be fallacious to this extent, that neither will the horizontal motion be uniform nor the natural acceleration be in the ratio assumed, nor the path of the projectile a parabola, etc. But, on the other hand, I ask you not to begrudge our Author that which other eminent men have assumed even if not strictly true. The authority of Archimedes alone will satisfy everybody. In his Mechanics and in his first quadrature of the parabola he takes for granted that the beam of a balance or steelyard is a straight line, every point of which is equidistant from the common center of all heavy bodies, and that the cords by which heavy bodies are suspended are parallel to each other.
Some consider this assumption permissible because, in practice, our instruments and the distances involved are so small in comparison with the enormous distance from the center of the earth that we may consider a minute of arc on a great circle as a straight line, and may regard the perpendiculars let fall from its two extremities as parallel. For if in actual practice one had to consider such small quantities, it would be necessary first of all to criticize the architects who presume, by use of a plumbline, to erect high towers with parallel sides. I may add that, in all their discussions, Archimedes and the others considered themselves as located at an infinite distance from the center of the earth, in which case their assumptions were not false, and therefore their conclusions were absolutely correct. When we wish to apply our proven conclusions to distances which, though finite, are very large, it is necessary for us to infer, on the basis of demonstrated truth, what correction is to be made for the fact that our distance from the center of the earth is not really infinite, but merely very great in comparison with the small dimensions of our apparatus. The largest of these will be the range of our projectiles--and even here we need consider only the artillery, which, however great, will never exceed four of those miles of which as many thousand separate us from the center of the earth; and since these paths terminate upon the surface of the earth only very slight changes can take place in their parabolic figure which, it is conceded, would be greatly altered if they terminated at the center of the earth.
As to the perturbation arising from the resistance of the medium this is more considerable and does not, on account of its manifold forms, submit to fixed laws and exact description. Thus if we consider only the resistance which the air offers to the motions studied by us, we shall see that it disturbs them all and disturbs them in an infinite variety of ways corresponding to the infinite variety in the form, weight, and velocity of the projectiles. For as to velocity, the greater this is, the greater will be the resistance offered by the air; a resistance which will be greater as the moving bodies become less dense. So that although the falling body ought to be displaced in proportion to the square of the duration of its motion, yet no matter how heavy the body, if it falls from a very considerable height, the resistance of the air will be such as to prevent any increase in speed and will render the motion uniform; and in proportion as the moving body is less dense this uniformity will be so much the more quickly attained and after a shorter fall. Even horizontal motion which, if no impediment were offered, would be uniform and constant is altered by the resistance of the air and finally ceases; and here again the less dense the body the quicker the process. Of these properties of weight, of velocity, and also of form, infinite in number, it is not possible to give any exact description; hence, in order to handle this matter in a scientific way, it is necessary to cut loose from these difficulties; and having discovered and demonstrated the theorems, in the case of no resistance, to use them and apply them with such limitations as experience will teach. And the advantage of this method will not be small; for the material and shape of the projectile may be chosen, as dense and round as possible, so that it will encounter the least resistance in the medium. Nor will the spaces and velocities in general be so great but that we shall be easily able to correct them with precision.
In the case of those projectiles which we use, made of dense material and round in shape, or of lighter material and cylindrical in shape, such as arrows, thrown from a sling or crossbow, the deviation from an exact parabolic path is quite insensible. Indeed, it you will allow me a little greater liberty, I can show you, by two experiments, that the dimensions of our apparatus are so small that these external and incidental resistances, among which that of the medium is the most considerable, are scarcely observable.
I now proceed to the consideration of motions through the air, since it is with these that we are now especially concerned; the resistance of the air exhibits itself in two ways: first by offering greater impedance to less dense than to very dense bodies, and secondly by offering greater resistance to a body in rapid motion than to the same body in slow motion.
Regarding the first of these, consider the case of two balls having the same dimensions, but one weighing ten or twelve times as much as the other; one, say, of lead, the other of oak, both allowed to fall from an elevation of 150 or 200 cubits.
Experiment shows that they will reach the earth with slight difference in speed, showing us that in both cases the retardation caused by the air is small; for if both balls start at the same moment and at the same elevation, and if the leaden one be slightly retarded and the wooden one greatly retarded, then the former ought to reach the earth a considerable distance in advance of the latter, since it is ten times as heavy. But this does not happen; indeed, the gain in distance of one over the other does not amount to the hundredth part of the entire fall. And in the case of a ball of stone weighing only a third or half as much as one of lead, the difference in their times of reaching the earth will be scarcely noticeable. Now since the speed acquired by a leaden ball in falling from a height of 200 cubits is so great that if the motion remained uniform the ball would, in an interval of time equal to that of the fall, traverse 400 cubits, and since this speed is so considerable in comparison with those which, by use of bows or other machines except fire arms, we are able to give to our projectiles, it follows that we may, without sensible error, regard as absolutely true those propositions which we are about to prove without considering the resistance of the medium.