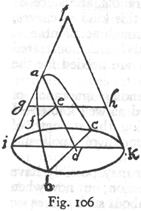Two New Sciences, pp. 1-61

Brackets: ( ) page numbers for Dover Edition (Crew and de Salvio) ; [ ] paging in National Edition

Two New Sciences, pp. 244-279

FOURTH DAY

SALVIATI. Once more, Simplicio is here on time; so let us without delay take up the question of motion. The text of our Author follows:

THE MOTION OF PROJECTILES

In the preceding pages we have discussed the properties of uniform motion and of motion naturally accelerated along planes of all inclinations. I now propose to set forth those properties which belong to a body whose motion is compounded of two other motions, namely, one uniform and one naturally accelerated; these properties, well worth knowing, I propose to demonstrate in a rigid manner. This is the kind of motion seen in a moving projectile; its origin I conceive to be as follows:

Imagine any particle projected along a horizontal plane without friction; then we know, from what has been more fully explained in the preceding pages, that this particle will move along this same plane with a motion which is uniform and perpetual, provided the plane has no limits. But if the plane is limited and elevated, then the moving particle, which we imagine to be a heavy one, will on passing over the edge of the plane acquire, in addition to its previous uniform and perpetual motion, a downward propensity due to its own weight; so that the resulting motion which I call projection [projectio] is compounded of one which is uniform and horizontal and of another which is vertical and naturally accelerated. We now proceed to (245) demonstrate some of its properties, the first of which is as follows: [269]

THEOREM 1, PROPOSITION I

A projectile which is carried by a uniform horizontal motion compounded with a naturally accelerated vertical motion describes a path which is a semi-parabola.

SAGR. Here, Salviati, it will be necessary to stop a little while for my sake and, I believe, also for the benefit of Simplicio; for it so happens that I have not gone very far in my study of Apollonius and am merely aware of the fact that he treats of the parabola and other conic sections, without an understanding of which I hardly think one will be able to follow the proof of other propositions depending upon them. Since even in this first beautiful theorem the author finds it necessary to prove that the path of a projectile is a parabola, and since, as I imagine, we shall have to deal with only this kind of curves, it will be absolutely necessary to have a thorough acquaintance, if not with all the properties which Apollonius has demonstrated for these figures, at least with those which are needed for the present treatment.

SAGR. You are quite too modest, pretending ignorance of facts which not long ago you acknowledged as well known -- I mean at the time when we were discussing the strength of materials and needed to use a certain theorem of Apollonius which gave you no trouble.

SAGR. I may have chanced to know it or may possibly have assumed it, so long as needed, for that discussion; but now when we have to follow all these demonstrations about such curves we ought not, as they say, to swallow it whole, and thus waste time and energy.

SIMP. Now even though Sagredo is, as I believe, well equipped for all his needs, I do not understand even the elementary terms; for although our philosophers have treated the motion of projectiles, I do not recall their having described the path of a projectile except to state in a general way that it is always a (246) curved line, unless the projection be vertically upwards. But [270] if the little Euclid which I have learned since our previous discussion does not enable me to understand the demonstrations which are to follow, then I shall be obliged to accept the theorems on faith without fully comprehending them.

SALV. On the contrary, I desire that you should understand them from the Author himself, who, when he allowed me to see this work of his, was good enough to prove for me two of the principal properties of the parabola because I did not happen to have at hand the books of Apollonius. These properties, which are the only ones we shall need in the present discussion, he proved in such a way that no prerequisite knowledge was required. These theorems are, indeed, given by Apollonius, but after many preceding ones, to follow which would take a long while. I wish to shorten our task by deriving the first property purely and simply from the mode of generation of the parabola and proving the second immediately from the first.

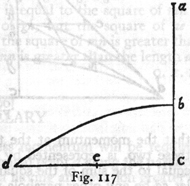
Beginning now with the first, imagine a right cone, erected upon the circular base ibkc with apex at l. The section of this cone made by a plane drawn parallel to the side lk is the curve which is called a parabola. The base of this parabola bc cuts at right angles the diameter ik of the circle ibkc, and the axis ad is parallel to the side lk; now having taken any point f in the curve bfa draw the straight line fe parallel to bd; then, I say, the square of bd is to the square of fe in the same ratio as the axis ad is to the portion ae. Through the point e pass a plane parallel to the circle ibkc, producing in the cone a circular section whose diameter is the line geh. Since bd is at right angles to ik in the circle ibk, the square of bd is equal to the rectangle formed by id and dk; so also in the upper circle which passes through the points gfh the square of fe is equal to the rectangle formed by (247) ge and eh; hence the square of bd is to the square of fe as the rectangle id. dk is to the rectangle ge. eh. And since the line ed is parallel to hk, the line eh, being parallel to dk, is equal to it; therefore the rectangle id. dk is to the rectangle ge. eh as id is to [271] ge, that is, as da is to ae; whence also the rectangle id. dk is to the rectangle ge. eh, that is, the square of bd is to the square of fe, as the axis da is to the portion ae. Q. E. D.

The other proposition necessary for this discussion we demonstrate as follows. Let us draw a parabola whose axis ca is prolonged upwards to a point d; from any point b draw the line bc parallel to the base of the parabola; if now the point d is chosen so that da = ca, then, I say, the straight line drawn through the points b and d will be tangent to the parabola at b. For imagine, if possible, that this line cuts the parabola above or that its prolongation cuts it below, and through any point g in it draw the straight line fge. And since the square of fe is greater than the square of ge, the square of fe will bear a greater ratio to the square of bc than the square of ge to that of bc; and since, by the preceding proposition, the square of fe is to that of bc as the line ea is to ca, it follows that the line ea will bear to the line ca a greater ratio than the square of ge to that of bc, or, than the square of ed to that of cd (the sides of the triangles deg and dcb being proportional). But the line ea is to ca, or da, in the same ratio as four times the rectangle ea. ad is to four times the square of ad, or, what is the same, the square of cd, since this is four times the square of ad; hence four times the rectangle ea. ad bears to the square of cd (248) a greater ratio than the square of ed to the square of cd; but that would make four times the rectangle ea. ad greater than the square of ed; which is false, the fact being just the opposite, because the two portions ea and ad of the line ed are not equal. Therefore the line db touches the parabola without cutting it. Q. E. D.

SIMP. Your demonstration proceeds too rapidly and, it seems to me, you keep on assuming that all of Euclid's theorems are [272] as familiar and available to me as his first axioms, which is far from true. And now this fact which you spring upon us, that four times the rectangle ea. ad is less than the square of de because the two portions ea and ad of the line de are not equal brings me little composure of mind, but rather leaves me in suspense.

SALV. Indeed, all real mathematicians assume on the part of the reader perfect familiarity with at least the elements of Euclid; and here it is necessary in your case only to recall a proposition of the Second Book in which he proves that when a line is cut into equal and also into two unequal parts, the rectangle formed on the unequal parts is less than that formed on the equal (i. e. , less than the square on half the line), by an amount which is the square of the difference between the equal and unequal segments. From this it is clear that the square of the whole line which is equal to four times the square of the half is greater than four times the rectangle of the unequal parts. In order to understand the following portions of this treatise it will be necessary to keep in mind the two elemental theorems from conic sections which we have just demonstrated; and these two theorems are indeed the only ones which the Author uses. We can now resume the text and see how he demonstrates his first proposition in which he shows that a body falling with a motion compounded of a uniform horizontal and a naturally accelerated [naturale descendente] one describes a semi-parabola.

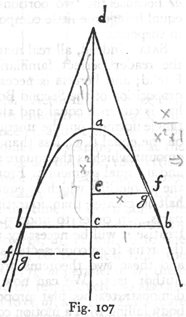
Let us imagine an elevated horizontal line or plane ab along which a body moves with uniform speed from a to b. Suppose (249) this plane to end abruptly at b; then at this point the body will, on account of its weight, acquire also a natural motion downwards along the perpendicular bn. Draw the line be along the plane ba to represent the flow, or measure, of time; divide this line into a number of segments, bc, cd, de, representing equal intervals of time; from the points b, c, d, e, let fall lines which are parallel to the perpendicular bn. On the first of these lay off any distance ci, on the second a distance four times as long, df; on [273] the third, one nine times as long, eh; and so on, in proportion to the squares of cb, db, eb, or, we may say, in the squared ratio of these same lines. Accordingly we see that while the body moves from b to c with uniform speed, it also falls perpendicularly through the distance ci, and at the end of the time-interval bc finds itself at the point i. In like manner at the end of the time-interval bd, which is the double of bc, the vertical fall will be four times the first distance ci; for it has been shown in a previous discussion that the distance traversed by a freely falling body varies as the square of the time; in like manner the space eh traversed during the time be will be nine times ci; thus it is evident that the distances eh, df, cl will be to one another as the squares of the lines be, bd, bc. Now from the points i, f, h draw the straight lines io, fg, hl parallel to be; these lines hl, fg, io are equal to eb, db and cb, respectively; so also are the lines bo, bg, bl respectively equal to ci, df, and eh. The square of hl is to that of fg as the line lb is to bg; and the square of fg is to that of io as gb is to bo; therefore the points i, f, h, lie on one and the same parabola. In like manner it may be shown that, if we take equal time-intervals of any size whatever, and if we imagine the particle to be carried by a similar compound motion, (250) the positions of this particle, at the ends of these time-intervals, will lie on one and the same parabola. Q. E. D.

SALV. This conclusion follows from the converse of the first of the two propositions given above. For, having drawn a parabola through the points b and h, any other two points, f and i, not falling on the parabola must lie either within or without; consequently the line fg is either longer or shorter than the line which terminates on the parabola. Therefore the square of hl will not bear to the square of fg the same ratio as the line lb to bg, but a greater or smaller; the fact is, however, that the square of hl does bear this same ratio to the square of fg. Hence the point f does lie on the parabola, and so do all the others.

SAGR. One cannot deny that the argument is new, subtle and conclusive, resting as it does upon this hypothesis, namely, that the horizontal motion remains uniform, that the vertical motion continues to be accelerated downwards in proportion to the square of the time, and that such motions and velocities as these combine without altering, disturbing, or hindering each other,^* so that as the motion proceeds the path of the projectile does not change into a different curve: but this, in my opinion, [274] is impossible. For the axis of the parabola along which we imagine the natural motion of a falling body to take place stands perpendicular to a horizontal surface and ends at the center of the earth; and since the parabola deviates more and more from its axis no projectile can ever reach the center of the earth or, if it does, as seems necessary, then the path of the projectile must transform itself into some other curve very different from the parabola.

SIMP. To these difficulties, I may add others. One of these is that we suppose the horizontal plane, which slopes neither up nor down, to be represented by a straight line as if each point on this line were equally distant from the center, which is not the case; for as one starts from the middle [of the line] and goes toward either end, he departs farther and farther from the center [of the earth] and is therefore constantly going uphill. Whence it follows that the motion cannot remain uniform (251) through any distance whatever, but must continually diminish. Besides, I do not see how it is possible to avoid the resistance of the medium which must destroy the uniformity of the horizontal motion and change the law of acceleration of falling bodies. These various difficulties render it highly improbable that a result derived from such unreliable hypotheses should hold true in practice.

SALV. All these difficulties and objections which you urge are so well founded that it is impossible to remove them; and, as for me, I am ready to admit them all, which indeed I think our author would also do. I grant that these conclusions proved in the abstract will be different when applied in the concrete and will be fallacious to this extent, that neither will the horizontal motion be uniform nor the natural acceleration be in the ratio assumed, nor the path of the projectile a parabola, etc. But, on the other hand, I ask you not to begrudge our Author that which other eminent men have assumed even if not strictly true. The authority of Archimedes alone will satisfy everybody. In his Mechanics and in his first quadrature of the parabola he takes for granted that the beam of a balance or steelyard is a straight line, every point of which is equidistant from the common center of all heavy bodies, and that the cords by which heavy bodies are suspended are parallel to each other.

Some consider this assumption permissible because, in practice, our instruments and the distances involved are so small in comparison with the enormous distance from the center of the earth that we may consider a minute of arc on a great circle as a straight line, and may regard the perpendiculars let fall from its two extremities as parallel. For if in actual practice one had to [275] consider such small quantities, it would be necessary first of all to criticise the architects who presume, by use of a plumbline, to erect high towers with parallel sides. I may add that, in all their discussions, Archimedes and the others considered themselves as located at an infinite distance from the center of the earth, in which case their assumptions were not false, and therefore their conclusions were absolutely correct. When we (251) wish to apply our proven conclusions to distances which, though finite, are very large, it is necessary for us to infer, on the basis of demonstrated truth, what correction is to be made for the fact that our distance from the center of the earth is not really infinite, but merely very great in comparison with the small dimensions of our apparatus. The largest of these will be the range of our projectiles -- and even here we need consider only the artillery -- which, however great, will never exceed four of those miles of which as many thousand separate us from the center of the earth; and since these paths terminate upon the surface of the earth only very slight changes can take place in their parabolic figure which, it is conceded, would be greatly altered if they terminated at the center of the earth.

As to the perturbation arising from the resistance of the medium this is more considerable and does not, on account of its manifold forms, submit to fixed laws and exact description. Thus if we consider only the resistance which the air offers to the motions studied by us, we shall see that it disturbs them all and disturbs them in an infinite variety of ways corresponding to the infinite variety in the form, weight, and velocity of the projectiles. For as to velocity, the greater this is, the greater will be the resistance offered by the air; a resistance which will be greater as the moving bodies become less dense [men gravi]. So that although the falling body ought to be displaced [andare accelerandosi] in proportion to the square of the duration of its motion, yet no matter how heavy the body, if it falls from a very considerable height, the resistance of the air will be such as to prevent any increase in speed and will render the motion [276] uniform; and in proportion as the moving body is less dense [men grave] this uniformity will be so much the more quickly attained and after a shorter fall. Even horizontal motion which, if no impediment were offered, would be uniform and constant is altered by the resistance of the air and finally ceases; and here again the less dense [piu leggiero] the body the quicker the process. Of these properties [accidenti] of weight, of velocity, and also of form [figura], infinite in number, it is not possible to give any exact description; hence, in order to handle this matter in a scientific way, it is necessary to cut loose from these difficulties; and having discovered and demonstrated the theorems, in the case of no resistance, to use them and apply them with such limitations as experience will teach. And the advantage of this method will not be small; for the material and shape of the projectile may be chosen, as dense and round as possible, so that it will encounter the least resistance in the medium. Nor will the spaces and velocities in general be so great but that we shall be easily able to correct them with precision.

In the case of those projectiles which we use, made of dense [grave] material and round in shape, or of lighter material and cylindrical in shape, such as arrows, thrown from a sling or crossbow, the deviation from an exact parabolic path is quite insensible. Indeed, it you will allow me a little greater liberty, I can show you, by two experiments, that the dimensions of our apparatus are so small that these external and incidental resistances, among which that of the medium is the most considerable, are scarcely observable.

I now proceed to the consideration of motions through the air, since it is with these that we are now especially concerned; the resistance of the air exhibits itself in two ways: first by offering greater impedance to less dense than to very dense bodies, and secondly by offering greater resistance to a body in rapid motion than to the same body in slow motion.

Regarding the first of these, consider the case of two balls having the same dimensions, but one weighing ten or twelve times as much as the other; one, say, of lead, the other of oak, both allowed to fall from an elevation of 150 or 200 cubits.

Experiment shows that they will reach the earth with slight difference in speed, showing us that in both cases the retardation caused by the air is small; for if both balls start at the same moment and at the same elevation, and if the leaden one be slightly retarded and the wooden one greatly retarded, then the former ought to reach the earth a considerable distance in advance of the latter, since it is ten times as heavy. But this [277] (254) does not happen; indeed, the gain in distance of one over the other does not amount to the hundredth part of the entire fall. And in the case of a ball of stone weighing only a third or half as much as one of lead, the difference in their times of reaching the earth will be scarcely noticeable. Now since the speed [impeto] acquired by a leaden ball in falling from a height of 200 cubits is so great that if the motion remained uniform the ball would, in an interval of time equal to that of the fall, traverse 400 cubits, and since this speed is so considerable in comparison with those which, by use of bows or other machines except fire arms, we are able to give to our projectiles, it follows that we may, without sensible error, regard as absolutely true those propositions which we are about to prove without considering the resistance of the medium.

Passing now to the second case, where we have to show that the resistance of the air for a rapidly moving body is not very much greater than for one moving slowly, ample proof is given by the following experiment. Attach to two threads of equal length -- say four or five yards -- two equal leaden balls and suspend them from the ceiling; now pull them aside from the perpendicular, the one through 80 or more degrees, the other through not more than four or five degrees; so that, when set free, the one falls, passes through the perpendicular, and describes large but slowly decreasing arcs of 160, 150, 140 degrees, etc. ; the other swinging through small and also diminishing arcs of 10, 8, 6, degrees, etc.

In the first place it must be remarked that one pendulum passes through its arcs of 180°, 160°, etc. , in the same time that the other swings through its 10°, 8°, etc. , from which it follows that the speed of the first ball is 16 and 18 times greater than that of the second. Accordingly, if the air offers more resistance to the high speed than to the low, the frequency of vibration in the large arcs of 180° or 160°, etc. , ought to be less than in the small arcs of 10°, 8°, 4°, etc. , and even less than in arcs of 2°, or 1°; but this prediction is not verified by experiment; because if two persons start to count the vibrations, the one the large, the other the small, they will discover that after counting tens (255) and even hundreds they will not differ by a single vibration, not even by a fraction of one. [278]

This observation justifies the two following propositions, namely, that vibrations of very large and very small amplitude all occupy the same time and that the resistance of the air does not affect motions of high speed more than those of low speed, contrary to the opinion hitherto generally entertained.

SAGR. On the contrary, since we cannot deny that the air hinders both of these motions, both becoming slower and finally vanishing, we have to admit that the retardation occurs in the same proportion in each case. But how? How, indeed, could the resistance offered to the one body be greater than that offered to the other except by the impartation of more momentum and speed [impeto e velocità] to the fast body than to the slow? And if this is so the speed with which a body moves is at once the cause and measure [cagione e misura] of the resistance which it meets. Therefore, all motions, fast or slow, are hindered and diminished in the same proportion; a result, it seems to me, of no small importance.

SALV. We are able, therefore, in this second case to say that the errors, neglecting those which are accidental, in the results which we are about to demonstrate are small in the case of our machines where the velocities employed are mostly very great and the distances negligible in comparison with the semidiameter of the earth or one of its great circles.

SIMP. I would like to hear your reason for putting the projectiles of fire arms, i.e., those using powder, in a different class from the projectiles employed in bows, slings, and crossbows, on the ground of their not being equally subject to change and resistance from the air.

SALV. I am led to this view by the excessive and, so to speak, supernatural violence with which such projectiles are launched; for, indeed, it appears to me that without exaggeration one might say that the speed of a ball fired either from a musket or from a piece of ordnance is supernatural. For if such a ball be allowed to fall from some great elevation its speed will, owing to the (256) resistance of the air, not go on increasing indefinitely; that which happens to bodies of small density in falling through short distances -- I mean the reduction of their motion to uniformity -- will also happen to a ball of iron or lead after it has fallen a few thousand cubits; this terminal or final speed [terminata velocità] is the maximum which such a heavy body can naturally acquire [279] in falling through the air. This speed I estimate to be much smaller than that impressed upon the ball by the burning powder.

An appropriate experiment will serve to demonstrate this fact. From a height of one hundred or more cubits fire a gun [archibuso] loaded with a lead bullet, vertically downwards upon a stone pavement; with the same gun shoot against a similar stone from a distance of one or two cubits, and observe which of the two balls is the more flattened. Now if the ball which has come from the greater elevation is found to be the less flattened of the two, this will show that the air has hindered and diminished the speed initially imparted to the bullet by the powder, and that the air will not permit a bullet to acquire so great a speed, no matter from what height it falls; for if the speed impressed upon the ball by the fire does not exceed that acquired by it in falling freely [naturalmente] then its downward blow ought to be greater rather than less.

This experiment I have not performed, but I am of the opinion that a musket-ball or cannon-shot, falling from a height as great as you please, will not deliver so strong a blow as it would if fired into a wall only a few cubits distant, i.e., at such a short range that the splitting or rending of the air will not be sufficient to rob the shot of that excess of supernatural violence given it by the powder.

The enormous momentum [impeto] of these violent shots may cause some deformation of the trajectory, making the beginning of the parabola flatter and less curved than the end; but, so far as our Author is concerned, this is a matter of small consequence in practical operations, the main one of which is the preparation of a table of ranges for shots of high elevation, giving the distance (257) attained by the ball as a function of the angle of elevation; and since shots of this kind are fired from mortars [mortari] using small charges and imparting no supernatural momentum [impeto sopranaturale] they follow their prescribed paths very exactly.

But now let us proceed with the discussion in which the Author invites us to the study and investigation of the motion of a body [impeto del mobile] when that motion is compounded of two others; and first the case in which the two are uniform, the one horizontal, the other vertical. [280]

THEOREM II, PROPOSITION II

When the motion of a body is the resultant of two uniform motions, one horizontal, the other perpendicular, the square of the resultant momentum is equal to the sum of the squares of the two component momenta. *

Let us imagine any body urged by two uniform motions and let ab represent the vertical displacement, while bc represents the displacement which, in the same interval of time, takes place in a horizontal direction. If then the distances ab and bc are traversed, during the same time-interval, with uniform motions the corresponding momenta will be to each other as the distances ab and bc are to each other; but the body which is urged by these two motions describes the diagonal ac; its momentum is proportional to ac. Also the square of ac is equal to the sum of the squares of ab and bc. Hence the square of the resultant momentum is equal to the sum of the squares of the two momenta ab and bc. Q. E. D.

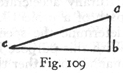
SIMP. At this point there is just one slight difficulty which needs to be cleared up; for it seems to me that the conclusion (258) just reached contradicts a previous proposition* in which it is claimed that the speed [impeto] of a body coming from a to b is equal to that in coming from a to c; while now you conclude that the speed [impeto] at c is greater than that at b.

SALV. Both propositions, Simplicio, are true, yet there is a great difference between them. Here we are speaking of a body urged by a single motion which is the resultant of two uniform motions, while there we were speaking of two bodies each urged with naturally accelerated motions, one along the vertical ab the other along the inclined plane ac. Besides the time-intervals were there not supposed to be equal, that along the incline ac being greater than that along the vertical ab; but the motions of which we now speak, those along ab, bc, ac, are uniform and simultaneous.

SIMP. Pardon me; I am satisfied; pray go on. [281]

SALV. Our Author next undertakes to explain what happens when a body is urged by a motion compounded of one which is horizontal and uniform and of another which is vertical but naturally accelerated; from these two components results the path of a projectile, which is a parabola. The problem is to determine the speed [impeto] of the projectile at each point. With this purpose in view our Author sets forth as follows the manner, or rather the method, of measuring such speed [impeto] along the path which is taken by a heavy body starting from rest and falling with a naturally accelerated motion.

THEOREM III, PROPOSITION III

Let the motion take place along the line ab, starting from rest at a, and in this line choose any point c. Let ac represent the time, or the measure of the time, required for the body to fall through the space ac; let ac also represent the velocity [impetus seu momentum] at c acquired by a fall through the distance ac. In the line ab select any other point b. The problem now is to determine the velocity at b acquired by a body in falling through the distance ab and to express this in terms of the velocity at c, the measure of which is the length ac. Take (259) as a mean proportional between ac and ab. We shall prove that the velocity at b is to that at c as the length as is to the length ac. Draw the horizontal line cd, having twice the length of ac, and be, having twice the length of ba. It then follows, from the preceding theorems, that a body falling through the distance ac, and turned so as to move along the horizontal cd with a uniform speed equal to that acquired on reaching c [282] will traverse the distance cd in the same interval of time as that required to fall with accelerated motion from a to c. Likewise be will be traversed in the same time as ba. But the time of descent through ab is as; hence the horizontal distance be is also traversed in the time as. Take a point l such that the time as is to the time ac as be is to bl; since the motion along be is uniform, the distance bl, if traversed with the speed [momentum celeritatis] acquired at b, will occupy the time ac; but in this same time-interval, ac, the distance cd is traversed with the speed acquired in c. Now two speeds are to each other as the distances traversed in equal intervals of time. Hence the speed at c is to the speed at b as cd is to bl. But since dc is to be as their halves, namely, as ca is to ba, and since be is to bl as ba is to sa; it follows that dc is to bl as ca is to sa. In other words, the speed at c is to that at b as ca is to sa, that is, as the time of fall through ab.

The method of measuring the speed of a body along the direction of its fall is thus clear; the speed is assumed to increase directly as the time.

But before we proceed further, since this discussion is to deal with the motion compounded of a uniform horizontal one and one accelerated vertically downwards -- the path of a projectile, namely, a parabola -- it is necessary that we define some common standard by which we may estimate the velocity, or momentum [velocitatem, impetum seu momentum] of both motions; (260) and since from the innumerable uniform velocities one only, and that not selected at random, is to be compounded with a velocity acquired by naturally accelerated motion, I can think of no simpler way of selecting and measuring this than to assume another of the same kind. * For the sake of clearness, draw the vertical line ac to meet the horizontal line bc. Ac is the height and bc the amplitude of the semi-parabola ab, which is the resultant of the two motions, one that of a body falling [283] from rest at a, through the distance ac, with naturally accelerated motion, the other a uniform motion along the horizontal ad. The speed acquired at c by a fall through the distance ac is determined by the height ac; for the speed of a body falling from the same elevation is always one and the same; but along the horizontal one may give a body an infinite number of uniform speeds. However, in order that I may select one out of this multitude and separate it from the rest in a perfectly definite manner, I will extend the height ca upwards to e just as far as is necessary and will call this distance ae the "sublimity. " Imagine a body to fall from rest at e; it is clear that we may make its terminal speed at a the same as that with which the same body travels along the horizontal line ad; this speed will be such that, in the time of descent along ea, it will describe a horizontal distance twice the length of ea. This preliminary remark seems necessary.

The reader is reminded that above I have called the horizontal line cb the "amplitude" of the semi-parabola ab; the axis ac of this parabola, I have called its "altitude"; but the line ea the fall along which determines the horizontal speed I have called the "sublimity. " These matters having been explained, I proceed with the demonstration. (261)

SAGR. Allow me, please, to interrupt in order that I may point out the beautiful agreement between this thought of the Author and the views of Plato concerning the origin of the various uniform speeds with which the heavenly bodies revolve. The latter chanced upon the idea that a body could not pass from rest to any given speed and maintain it uniformly except by passing through all the degrees of speed intermediate between the given speed and rest. Plato thought that God, after having created the heavenly bodies, assigned them the proper and uniform speeds with which they were forever to revolve; and that He made them start from rest and move over definite distances under a natural and rectilinear acceleration such as governs the motion of terrestrial bodies. He added that once these bodies had gained their proper and permanent speed, their rectilinear motion was converted into a circular one, the only [284] motion capable of maintaining uniformity, a motion in which the body revolves without either receding from or approaching its desired goal. This conception is truly worthy of Plato; and it is to be all the more highly prized since its underlying principles remained hidden until discovered by our Author who removed from them the mask and poetical dress and set forth the idea in correct historical perspective. In view of the fact that astronomical science furnishes us such complete information concerning the size of the planetary orbits, the distances of these bodies from their centers of revolution, and their velocities, I cannot help thinking that our Author (to whom this idea of Plato was not unknown) had some curiosity to discover whether or not a definite "sublimity" might be assigned to each planet, such that, if it were to start from rest at this particular height and to fall with naturally accelerated motion along a straight line, and were later to change the speed thus acquired into uniform motion, the size of its orbit and its period of revolution would be those actually observed.

SALV. I think I remember his having told me that he once made the computation and found a satisfactory correspondence with observation. But he did not wish to speak of it, lest in (262) view of the odium which his many new discoveries had already brought upon him, this might be adding fuel to the fire. But if any one desires such information he can obtain it for himself from the theory set forth in the present treatment.

We now proceed with the matter in hand, which is to prove:

PROBLEM I, PROPOSITION IV

To determine the momentum of a projectile at each particular point in its given parabolic path.

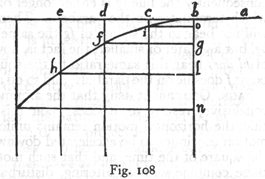
Let bec be the semi-parabola whose amplitude is cd and whose height is db, which latter extended upwards cuts the tangent of the parabola ca in a. Through the vertex draw the horizontal line bi parallel to cd. Now if the amplitude cd is equal to the entire height da, then bi will be equal to ba and also to bd; and if we take ab as the measure of the time required for fall through the distance ab and also of the momentum acquired at b in consequence of its fall from rest at a, then if we turn into a horizontal direction the momentum acquired by fall through ab [impetum ab] the space traversed in the same interval of time will be represented by dc which is twice bi. But a body which falls from rest at b along the line bd will during the same time-interval fall through the height of the parabola [285] bd. Hence a body falling from rest at a, turned into a horizontal direction with the speed ab will traverse a space equal to dc. Now if one superposes upon this motion a fall along bd, traversing the height bd while the parabola bc is described, then the momentum of the body at the terminal point c is the resultant of a uniform horizontal momentum, whose value is represented by ab, and of another momentum acquired by fall from b to the terminal point d or c; these two momenta are equal. If, therefore, we take ab to be the measure of one of these momenta, say, the uniform horizontal one, then bi, which is equal to bd, will represent the momentum acquired at d or c; and ia will represent the resultant of these two momenta, that is, the total momentum with which the projectile, travelling along the parabola, strikes at c. (263)

With this in mind let us take any point on the parabola, say e, and determine the momentum with which the projectile passes that point. Draw the horizontal ef and take bg a mean proportional between bd and bf. Now since ab, or bd, is assumed to be the measure of the time and of the momentum [momentum velocitatis] acquired by falling from rest at b through the distance bd, it follows that bg will measure the time and also the momentum [impetus] acquired at f by fall from b. If therefore we lay off bo, equal to bg, the diagonal line joining a and o will represent the momentum at the point e; because the length ab has been assumed to represent the momentum at b which, after diversion into a horizontal direction, remains constant; and because bo measures the momentum at f or e, acquired by fall, from rest at b, through the height bf. But the square of ao equals the sum of the squares of ab and bo. Hence the theorem sought.

SAGR. The manner in which you compound these different momenta to obtain their resultant strikes me as so novel that my mind is left in no small confusion. I do not refer to the composition of two uniform motions, even when unequal, and when one takes place along a horizontal, the other along a vertical direction; because in this case I am thoroughly convinced that the resultant is a motion whose square is equal to the sum of the squares of the two components. The confusion arises when one undertakes to compound a uniform horizontal motion with a vertical one which is naturally accelerated. I trust, therefore, we may pursue this discussion more at length. [286]

SIMP. And I need this even more than you since I am not yet as clear in my mind as I ought to be concerning those fundamental propositions upon which the others rest. Even in the (264) case of the two uniform motions, one horizontal, the other perpendicular, I wish to understand better the manner in which you obtain the resultant from the components. Now, Salviati, you understand what we need and what we desire.

SALV. Your request is altogether reasonable and I will see whether my long consideration of these matters will enable me to make them clear to you. But you must excuse me if in the explanation I repeat many things already said by the Author. Concerning motions and their velocities or momenta [movimenti e lor velocità o impeti] whether uniform or naturally accelerated, one cannot speak definitely until he has established a measure for such velocities and also for time. As for time we have the already widely adopted hours, first minutes and second minutes. So for velocities, just as for intervals of time, there is need of a common standard which shall be understood and accepted by everyone, and which shall be the same for all. As has already been stated, the Author considers the velocity of a freely falling body adapted to this purpose, since this velocity increases according to the same law in all parts of the world; thus for instance the speed acquired by a leaden ball of a pound weight starting from rest and falling vertically through the height of, say, a spear's length is the same in all places; it is therefore excellently adapted for representing the momentum [impeto] acquired in the case of natural fall.

It still remains for us to discover a method of measuring momentum in the case of uniform motion in such a way that all who discuss the subject will form the same conception of its size and velocity [grandezza e velocità]. This will prevent one person from imagining it larger, another smaller, than it really is; so that in the composition of a given uniform motion with one which is accelerated different men may not obtain different values for the resultant. In order to determine and represent such a momentum and particular speed [impeto e velocità particolare] our Author has found no better method than to use the momentum acquired by a body in naturally accelerated motion. [287]

The speed of a body which has in this manner acquired any (265) momentum whatever will, when converted into uniform motion, retain precisely such a speed as, during a time-interval equal to that of the fall, will carry the body through a distance equal to twice that of the fall. But since this matter is one which is fundamental in our discussion it is well that we make it perfectly clear by means of some particular example.

Let us consider the speed and momentum acquired by a body falling through the height, say, of a spear [picca] as a standard which we may use in the measurement of other speeds and momenta as occasion demands; assume for instance that the time of such a fall is four seconds [minuti secondi d'ora]; now in order to measure the speed acquired from a fall through any other height, whether greater or less, one must not conclude that these speeds bear to one another the same ratio as the heights of fall; for instance, it is not true that a fall through four times a given height confers a speed four times as great as that acquired by descent through the given height; because the speed of a naturally accelerated motion does not vary in proportion to the time. As has been shown above, the ratio of the spaces is equal to the square of the ratio of the times.

If, then, as is often done for the sake of brevity, we take the same limited straight line as the measure of the speed, and of the time, and also of the space traversed during that time, it follows that the duration of fall and the speed acquired by the same body in passing over any other distance, is not represented by this second distance, but by a mean proportional between the two distances. This I can better illustrate by an example. In the vertical line ac, lay off the portion ab to represent the distance traversed by a body falling freely with accelerated motion: the time of fall may be represented by any limited straight line, but for the sake of brevity, we shall represent it by the same length ab; this length may also be employed as a measure of the momentum and speed acquired during the motion; in short, let ab be a measure of the various physical quantities which enter this discussion.

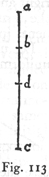
Having agreed arbitrarily upon ab as a measure of these (266) three different quantities, namely, space, time, and momentum, our next task is to find the time required for fall through a [288] given vertical distance ac, also the momentum acquired at the terminal point c, both of which are to be expressed in terms of the time and momentum represented by ab. These two required quantities are obtained by laying off ad, a mean proportional between ab and ac; in other words, the time of fall from a to c is represented by ad on the same scale on which we agreed that the time of fall from a to b should be represented by ab. In like manner we may say that the momentum [impeto o grado di velocità] acquired at c is related to that acquired at b, in the same manner that the line ad is related to ab, since the velocity varies directly as the time, a conclusion, which although employed as a postulate in Proposition III, is here amplified by the Author.

This point being clear and well-established we pass to the consideration of the momentum [impeto] in the case of two compound motions, one of which is compounded of a uniform horizontal and a uniform vertical motion, while the other is compounded of a uniform horizontal and a naturally accelerated vertical motion. If both components are uniform, and one at right angles to the other, we have already seen that the square of the resultant is obtained by adding the squares of the components [p. 257] as will be clear from the following illustration.

Let us imagine a body to move along the vertical ab with a uniform momentum [impeto] of 3, and on reaching b to move toward c with a momentum [velocità ed impeto] of 4, so that during the same time-interval it will traverse 3 cubits along the vertical and 4 along the horizontal. But a particle which moves with the resultant velocity [velocità] will, in the same time, traverse the diagonal ac, whose length is not 7 cubits -- the sum of ab (3) and bc (4) -- but 5, which is in potenza equal to the sum of 3 and 4, that is, the squares of 3 and 4 when added make 25, which is the square of ac, and is equal to the sum of the squares (267) of ab and bc. Hence ac is represented by the side -- or we may say the root -- of a square whose area is 25, namely 5.

As a fixed and certain rule for obtaining the momentum which [289] results from two uniform momenta, one vertical, the other horizontal, we have therefore the following: take the square of each, add these together, and extract the square root of the sum, which will be the momentum resulting from the two. Thus, in the above example, the body which in virtue of its vertical motion would strike the horizontal plane with a momentum [forza] of 3, would owing to its horizontal motion alone strike at c with a momentum of 4; but if the body strikes with a momentum which is the resultant of these two, its blow will be that of a body moving with a momentum [velocità e forza] of 5; and such a blow will be the same at all points of the diagonal ac, since its components are always the same and never increase or diminish.

Let us now pass to the consideration of a uniform horizontal motion compounded with the vertical motion of a freely falling body starting from rest. It is at once clear that the diagonal which represents the motion compounded of these two is not a straight line, but, as has been demonstrated, a semi-parabola, in which the momentum [impeto] is always increasing because the speed [velocità] of the vertical component is always increasing. Wherefore, to determine the momentum [impeto] at any given point in the parabolic diagonal, it is necessary first to fix upon the uniform horizontal momentum [impeto] and then, treating the body as one falling freely, to find the vertical momentum at the given point; this latter can be determined only by taking into account the duration of fall, a consideration which does not enter into the composition of two uniform motions where the velocities and momenta are always the same; but here where one of the component motions has an initial value of zero and increases its speed [velocità] in direct proportion to the time, it follows that the time must determine the speed [velocità] at the assigned point. It only remains to obtain the momentum resulting from these two components (as in the case of uniform motions) by placing the square of the resultant equal (268) to the sum of the squares of the two components. But here again it is better to illustrate by means of an example.

On the vertical ac lay off any portion ab which we shall employ as a measure of the space traversed by a body falling freely along the perpendicular, likewise as a measure of the time and also of the speed [grado di velocità] or, we may say, of the momenta [impeti]. It is at once clear that if the momentum of a [290] body at b, after having fallen from rest at a, be diverted along the horizontal direction bd, with uniform motion, its speed will be such that, during the time-interval ab, it will traverse a distance which is represented by the line bd and which is twice as great as ab. Now choose a point c, such that bc shall be equal to ab, and through c draw the line ce equal and parallel to bd; through the points b and e draw the parabola bei. And since, during the time-interval ab, the horizontal distance bd or ce, double the length ab, is traversed with the momentum ab, and since during an equal time-interval the vertical distance bc is traversed, the body acquiring at c a momentum represented by the same horizontal, bd, it follows that during the time ab the body will pass from b to e along the parabola be, and will reach e with a momentum compounded of two momenta each equal to ab. And since one of these is horizontal and the other vertical, the square of the resultant momentum is equal to the sum of the squares of these two components, i. e. , equal to twice either one of them.

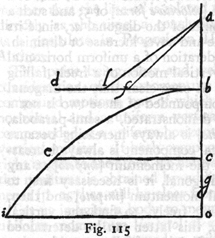
Therefore, if we lay off the distance bf, equal to ba, and draw the diagonal af, it follows that the momentum [impeto e percossa] at e will exceed that of a body at b after having fallen from (269) a, or what is the same thing, will exceed the horizontal momentum [percossa dell'impeto] along bd, in the ratio of af to ab.

Suppose now we choose for the height of fall a distance bo which is not equal to but greater than ab, and suppose that bg represents a mean proportional between ba and bo; then, still retaining ba as a measure of the distance fallen through, from rest at a, to b, also as a measure of the time and of the momentum which the falling body acquires at b, it follows that bg will be the measure of the time and also of the momentum which the body acquires in falling from b to o. Likewise just as the momentum ab during the time ab carried the body a distance along the horizontal equal to twice ab, so now, during the time-interval bg, the body will be carried in a horizontal direction through a distance which is greater in the ratio of bg to ba. Lay off lb equal to bg and draw the diagonal al, from which we have a quantity compounded of two velocities [impeti] one horizontal, the other vertical; these determine the parabola. The horizontal and uniform velocity is that acquired at b in falling from a; the other is that acquired at o, or, we may say, at i, by a body falling through the distance bo, during a time measured by the line bg, [291] which line bg also represents the momentum of the body. And in like manner we may, by taking a mean proportional between the two heights, determine the momentum [impeto] at the extreme end of the parabola where the height is less than the sublimity ab; this mean proportional is to be drawn along the horizontal in place of bf, and also another diagonal in place of af, which diagonal will represent the momentum at the extreme end of the parabola.

To what has hitherto been said concerning the momenta, blows or shocks of projectiles, we must add another very important consideration; to determine the force and energy of the shock [forza ed energia della percossa] it is not sufficient to consider only the speed of the projectiles, but we must also take into account the nature and condition of the target which, in no small degree, determines the efficiency of the blow. First of all it is well known that the target suffers violence from the speed (270) [velocità] of the projectile in proportion as it partly or entirely stops the motion; because if the blow falls upon an object which yields to the impulse [velocità del percuziente] without resistance such a blow will be of no effect; likewise when one attacks his enemy with a spear and overtakes him at an instant when he is fleeing with equal speed there will be no blow but merely a harmless touch. But if the shock falls upon an object which yields only in part then the blow will not have its full effect, but the damage will be in proportion to the excess of the speed of the projectile over that of the receding body; thus, for example, if the shot reaches the target with a speed of 10 while the latter recedes with a speed of 4, the momentum and shock [impeto e percossa] will be represented by 6. Finally the blow will be a maximum, in so far as the projectile is concerned, when the target does not recede at all but if possible completely resists and stops the motion of the projectile. I have said in so far as the projectile is concerned because if the target should approach the projectile the shock of collision [colpo e l'incontro] would be greater in proportion as the sum of the two speeds is greater than that of the projectile alone.

Moreover it is to be observed that the amount of yielding in the target depends not only upon the quality of the material, as regards hardness, whether it be of iron, lead, wool, etc. , but [292] also upon its position. If the position is such that the shot strikes it at right angles, the momentum imparted by the blow [impeto del colpo] will be a maximum; but if the motion be oblique, that is to say slanting, the blow will be weaker; and more and more so in proportion to the obliquity; for, no matter how hard the material of the target thus situated, the entire momentum [impeto e moto] of the shot will not be spent and stopped; the projectile will slide by and will, to some extent, continue its motion along the surface of the opposing body.

All that has been said above concerning the amount of momentum in the projectile at the extremity of the parabola must be understood to refer to a blow received on a line at right angles to this parabola or along the tangent to the parabola at the given (271) point; for, even though the motion has two components, one horizontal, the other vertical, neither will the momentum along the horizontal nor that upon a plane perpendicular to the horizontal be a maximum, since each of these will be received obliquely.

SAGR. Your having mentioned these blows and shocks recalls to my mind a problem, or rather a question, in mechanics of which no author has given a solution or said anything which diminishes my astonishment or even partly relieves my mind.

My difficulty and surprise consist in not being able to see whence and upon what principle is derived the energy and immense force [energia e forza immensa] which makes its appearance in a blow; for instance we see the simple blow of a hammer, weighing not more than 8 or 10 lbs. , overcoming resistances which, without a blow, would not yield to the weight of a body producing impetus by pressure alone, even though that body weighed many hundreds of pounds. I would like to discover a method of measuring the force [forza] of such a percussion. I can hardly think it infinite, but incline rather to the view that it has its limit and can be counterbalanced and measured by other forces, such as weights, or by levers or screws or other mechanical instruments which are used to multiply forces in a manner which I satisfactorily understand.

SALV. You are not alone in your surprise at this effect or in obscurity as to the cause of this remarkable property. I studied this matter myself for a while in vain; but my confusion merely increased until finally meeting our Academician I received from [293] him great consolation. First he told me that he also had for a long time been groping in the dark; but later he said that, after having spent some thousands of hours in speculating and contemplating thereon, he had arrived at some notions which are far removed from our earlier ideas and which are remarkable for their novelty. And since now I know that you would gladly hear what these novel ideas are I shall not wait for you to ask but promise that, as soon as our discussion of projectiles is completed, I will explain all these fantasies, or if you please, (272) vagaries, as far as I can recall them from the words of our Academician. In the meantime we proceed with the propositions of the author.

PROPOSITION V, PROBLEM

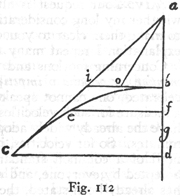
Having given a parabola, find the point, in its axis extended upwards, from which a particle must fall in order to describe this same parabola.

Let ab be the given parabola, hb its amplitude, and he its axis extended. The problem is to find the point e from which a body must fall in order that, after the momentum which it acquires at a has been diverted into a horizontal direction, it will describe the parabola ab. Draw the horizontal ag, parallel to bh, and having laid off af equal to ah, draw the straight line bf which will be a tangent to the parabola at b, and will intersect the horizontal ag at g: choose e such that ag will be a mean proportional between af and ae. Now I say that e is the point above sought. That is, if a body falls from rest at this point e, and if the momentum acquired at the point a be diverted into a horizontal direction, and compounded with the momentum acquired at h in falling from rest at a, then the body will describe the parabola ab. For if we understand ea to be the measure of the time of fall from e to a, and also of the momentum acquired at a, then ag (which is a mean proportional between ea and af) will represent the time and momentum of fall from f to a or, what is the same thing, from a to h; and since a body falling from e, during the time ea, will, owing to the momentum acquired at a, traverse at uniform speed a horizontal distance which is twice ea, it follows that, the body will if impelled by the same momentum, during the time-interval ag traverse a distance equal to twice ag which is the half of bh. This is true because, (273) in the case of uniform motion, the spaces traversed vary directly as the times. And likewise if the motion be vertical and start from rest, the body will describe the distance ah in the [294] time ag. Hence the amplitude bh and the altitude ah are traversed by a body in the same time. Therefore the parabola ab will be described by a body falling from the sublimity of e. Q.E.F.

COROLLARY

Hence it follows that half the base, or amplitude, of the semi-parabola (which is one-quarter of the entire amplitude) is a mean proportional between its altitude and the sublimity from which a falling body will describe this same parabola.

PROPOSITION VI, PROBLEM

Given the sublimity and the altitude of a parabola, to find its amplitude.

Let the line ac, in which lie the given altitude cb and sublimity ab, be perpendicular to the horizontal line cd. The problem is to find the amplitude, along the horizontal cd, of the semi-parabola which is described with the sublimity ba and altitude bc. Lay off cd equal to twice the mean proportional between cb and ba. Then cd will be the amplitude sought, as is evident from the preceding proposition.

THEOREM. PROPOSITION VII

If projectiles describe semi-parabolas of the same amplitude, the momentum required to describe that one whose amplitude is double its altitude is less than that required for any other.

(274)

Let bd be a semi-parabola whose amplitude cd is double its altitude cb; on its axis extended upwards lay off ba equal to its altitude bc. Draw the line ad which will be a tangent to the parabola at d and will cut the horizontal line be at the point e, making be equal to bc and also to ba. It is evident that this parabola will be described by a projectile whose uniform horizontal momentum is that which it would acquire at b in falling from rest at a and whose naturally accelerated vertical momentum is that of the body falling to c, from rest at b. From this it follows that the momentum at the terminal point d, compounded of these two, is represented by the diagonal ae, whose square is equal to the sum of the squares of the two components. Now let gd be any other parabola whatever having the same amplitude cd, but whose altitude cg is either greater or less than the altitude bc. Let hd be the tangent cutting the horizontal 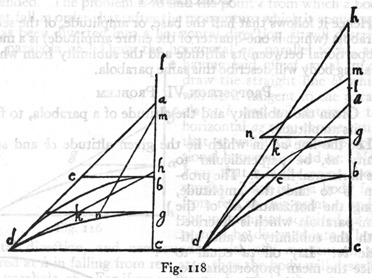[295] through g at k. Select a point l such that hg:gk =gk:gl. Then from a preceding proposition [V], it follows that gl will be the (275) height from which a body must fall in order to describe the parabola gd.

Let gm be a mean proportional between ab and gl; then gm will [Prop. IV] represent the time and momentum acquired at g by a fall from l; for ab has been assumed as a measure of both time and momentum. Again let gn be a mean proportional between bc and cg; it will then represent the time and momentum which the body acquires at c in falling from g. If now we join m and n, this line mn will represent the momentum at d of the projectile traversing the parabola dg, which momentum is, I say, greater than that of the projectile travelling along the parabola bd whose measure was given by ae. For since gn has been taken as a mean proportional between bc and gc; and since bc is equal to be and also to kg (each of them being the half of dc) it follows that cg:gn = gn:gk, and as cg or (hg) is to gk so is ng² to gk²: but by construction hg:gk = gk:gl. Hence ng²:gk² = gk:gl. But gk:gl = gk²:gm², since gm is a mean proportional between kg and gl. Therefore the three squares ng, kg, mg form a continued proportion, gn²:gk² = gk²:gm². And the sum of the two extremes which is equal to the square of mn is greater than twice the square of gk; but the square of ae is double the square of gk. Hence the square of mn is greater than the square of ae and the length mn is greater than the length ae. Q. E. D. [296]

COROLLARY

Conversely it is evident that less momentum will be required to send a projectile from the terminal point d along the parabola bd than along any other parabola having an elevation greater or less than that of the parabola bd, for which the tangent at d makes an angle of 45° with the horizontal. From which it follows that if projectiles are fired from the terminal point d, all having the same speed, but each having a different elevation, the maximum range, i.e., amplitude of the semi-parabola or of the entire parabola, will be obtained when the elevation is 45°: the (276) other shots, fired at angles greater or less will have a shorter range.

SAGR. The force of rigid demonstrations such as occur only in mathematics fills me with wonder and delight. From accounts given by gunners, I was already aware of the fact that in the use of cannon and mortars, the maximum range, that is the one in which the shot goes farthest, is obtained when the elevation is 45° or, as they say, at the sixth point of the quadrant; but to understand why this happens far outweighs the mere information obtained by the testimony of others or even by repeated experiment.

SALV. What you say is very true. The knowledge of a single fact acquired through a discovery of its causes prepares the mind to understand and ascertain other facts without need of recourse to experiment, precisely as in the present case, where by argumentation alone the Author proves with certainty that the maximum range occurs when the elevation is 45°. He thus demonstrates what has perhaps never been observed in experience, namely, that of other shots those which exceed or fall short of 45° by equal amounts have equal ranges; so that if the balls have been fired one at an elevation of 7 points, the other at 5, they will strike the level at the same distance: the same is true if the shots are fired at 8 and at 4 points, at 9 and at 3, etc. Now let us hear the demonstration of this. [297]

THEOREM. PROPOSITION VIII

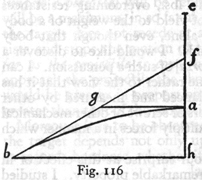
The amplitudes of two parabolas described by projectiles fired with the same speed, but at angles of elevation which exceed and fall short of 45° by equal amounts, are equal to each other.

In the triangle mcb let the horizontal side bc and the vertical cm, which form a right angle at c, be equal to each other; then the angle mbc will be a semi-right angle; let the line cm be prolonged to d, such a point that the two angles at b, namely mbe an mbd, one above and the other below the diagonal mb, shall be equal. It is now to be proved that in the case of two parabolas (277) described by two projectiles fired from b with the same speed, one at the angle of ebc, the other at the angle of dbc, their amplitudes will be equal. Now since the external angle bmc is equal to the sum of the internal angles mdb and dbm we may also equate to them the angle mbc; but if we replace the angle dbm by mbe, then this same angle mbc is equal to the two mbe and bdc: and if we subtract from each side of this equation the angle mbe, we have the remainder bdc equal to the remainder ebc. Hence the two triangles dcb and bce are similar. Bisect the straight lines dc and ec in the points h and f: and draw the lines hi and fg parallel to the horizontal cb, and choose l such that dh:hi = ih:hl. Then the triangle ihl will be similar to ihd, and also to the egf; and since ih and gf are equal, each being half of bc, it follows that hl is equal to fe and also to fc; and if we add to each of these the common part fh, it will be seen that ch is equal to fl.

Let us now imagine a parabola described through the points h and b whose altitude is hc and sublimity hl. Its amplitude will be cb which is double the length hi since hi is a mean proportional between dh (or ch) and hl. The line db is tangent to the parabola at b, since ch is equal to hd. If again we imagine a parabola described through the points f and b, with a sublimity fl and altitude fc, of which the mean proportional is fg, or one-half of cb, then, as before, will cb be the amplitude and the line eb a tangent at b; for ef and fc are equal. [298] But the two angles dbc and ebc, the angles of elevation, differ by equal amounts from a 45° angle. Hence follows the proposition.

THEOREM. PROPOSITION IX

The amplitudes of two parabolas are equal when their altitudes and sublimities are inversely proportional. (278)

Let the altitude gf of the parabola fh bear to the altitude cb of the parabola bd the same ratio which the sublimity ba bears to the sublimity fe, then I say the amplitude hg is equal to the amplitude dc. For since the first of these quantities, gf, bears to the second cb the same ratio which the third, ba, bears to the fourth fe, it follows that the area of the rectangle gf. fe is equal to that of the rectangle cb. ba; therefore squares which are equal to these rectangles are equal to each other. But [by Proposition VI] the square of half of gh is equal to the rectangle gf. fe; and the square of half of cd is equal to the rectangle cb. ba. Therefore these squares and their sides and the doubles of their sides are equal. But these last are the amplitudes gh and cd. Hence follows the proposition.

LEMMA FOR THE FOLLOWING PROPOSITION

If a straight line be cut at any point whatever and mean proportionals between this line and each of its parts be taken, the sum of the squares of these mean proportionals is equal to the square of the entire line.

Let the line ab be cut at c. Then I say that the square of the mean proportional between ab and ac plus the square of the mean proportional between ab and cb is equal to the square of the whole line ab. This is evident as soon as we describe a semicircle upon the entire line ab, erect a perpendicular cd at c, and draw da and db. For da is a mean proportional between ab and ac while [299] db is a mean proportional between ab and bc: and since the angle adb, inscribed in a semicircle, is a right angle the sum of (279) the squares of the lines da and db is equal to the square of the entire line ab. Hence follows the proposition.

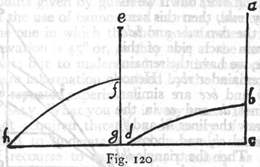
THEOREM. PROPOSITION X

The momentum [impetus seu momentum] acquired by a particle at the terminal point of any semi-parabola is equal to that which it would acquire in falling through a vertical distance equal to the sum of the sublimity and the altitude of the semi-parabola. *

Let ab be a semi-parabola having a sublimity da and an altitude ac, the sum of which is the perpendicular dc. Now I say the momentum of the particle at b is the same as that which it would acquire in falling freely from d to c. Let us take the length of dc itself as a measure of time and momentum, and lay off cf equal to the mean proportional between cd and da; also lay off ce a mean proportional between cd and ca. Now cf is the measure of the time and of the momentum acquired by fall, from rest at d, through the distance da; while ce is the time and momentum of fall, from rest at a, through the distance ca; also the diagonal, ef will represent a momentum which is the resultant of these two, and is therefore the momentum at the terminal point of the parabola, b.

And since dc has been cut at some point a and since cf and ce are mean proportionals between the whole of cd and its parts, da and ac, it follows, from the preceding lemma, that the sum of the squares of these mean proportionals is equal to the square of the whole: but the square of ef is also equal to the sum of these same squares; whence it follows that the line ef is equal to dc.

Accordingly the momentum acquired at c by a particle in falling from d is the same as that acquired at b by a particle traversing the parabola ab. Q. E. D.

index previous next