Particle in Anharmonic Potential

As a warm up before analyzing the driven damped anharmonic oscillator, we’ll explore the oscillations of a particle in an anharmonic potential

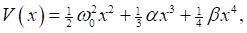
with no damping force and no driving force. Landau uses perturbation theory to predict that for oscillations of amplitude a, the frequency is approximately 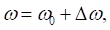where

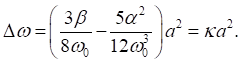
But just how good is this formula? We’ll find out.

Walk-Through

First set and check that the frequency doesn’t depend on amplitude: that is, on initial x, taking initial v = 0.
Next, set α = 0, 𝛽 = 5, set speed = 20, and try amplitudes (initial x's)= 0.1. Now go to initial x = 1, set speed = 2, and see how the frequency changes. Can you give a dimensional explanation? (Note that changing speed doesn't affect the physics, just the rate at which you see it.)

Next, set 𝛽 = 0 and take gradually increasing values of α, keeping the amplitude fixed. At some point, things will go bad. Why? Does the critical value of α depend on amplitude? Explain what's going on.

Now set ω₀² = -1, α = 0, 𝛽 = 5. This is the potential of the Duffing oscillator. Explore.

Here's the relevant lecture.

Program by: Carter Hedinger