Two New Sciences, pp. 1-61

Brackets: ( ) page numbers for Dover Edition (Crew and de Salvio) ; [ ] paging in National Edition

Two New Sciences, pp. 280-295

(280)

COROLLARY

Hence it follows that, in the case of all parabolas where the sum of the sublimity and altitude is a constant, the momentum at the terminal point is a constant.

PROBLEM. PROPOSITION XI

Given the amplitude and the speed [impetus] at the terminal point of a semi-parabola, to find its amplitude.

Let the given speed be represented by the vertical line ab, and the amplitude by the horizontal line bc; it is required to find the sublimity of the semi-parabola whose terminal speed is ab and amplitude bc. From what precedes [Cor. Prop. V] it is clear that half the amplitude bc is a mean proportional between [300] the altitude and sublimity of the parabola of which the terminal speed is equal, in accordance with the preceding proposition, to the speed acquired by a body in falling from rest at a through the distance ab. Therefore the line ba must be cut at a point such that the rectangle formed by its two parts will be equal to the square of half bc, namely bd. Necessarily, therefore, bd must not exceed the half of ba; for of all the rectangles formed by parts of a straight line the one of greatest area is obtained when the line is divided into two equal parts. Let e be the middle point of the line ab; and now if bd be equal to be the problem is solved; for be will be the altitude and ea the sublimity of the parabola. (Incidentally we may observe a consequence already demonstrated, namely: of all parabolas described with any given terminal speed that for which the elevation is 45 ° will have the maximum amplitude. )

But suppose that bd is less than half of ba which is to be (281) divided in such a way that the rectangle upon its parts may be equal to the square of bd. Upon ea as diameter describe a semi-circle efa, in which draw the chord af, equal to bd: join fe and lay off the distance eg equal to fe. Then the rectangle bg. ga plus the square of eg will be equal to the square of ea, and hence also to the sum of the squares of af and fe. If now we subtract the equal squares of fe and ge there remains the rectangle bg. ga equal to the square of af, that is, of bd, a line which is a mean proportional between bg and ga; from which it is evident that the semi-parabola whose amplitude is bc and whose terminal speed [impetus] is represented by ba has an altitude bg and a sublimity ga.

If however we lay off bi equal to ga, then bi will be the altitude of the semi-parabola ic, and ia will be its sublimity. From the preceding demonstration we are able to solve the following problem.

PROBLEM. PROPOSITION XII

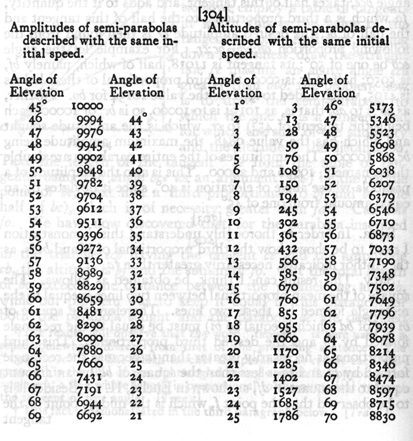
To compute and tabulate the amplitudes of all semi-parabolas which are described by projectiles fired with the same initial speed [impetus].

From the foregoing it follows that, whenever the sum of the altitude and sublimity is a constant vertical height for any set of parabolas, these parabolas are described by projectiles having the same initial speed; all vertical heights thus [301] obtained are therefore included between two parallel horizontal lines. Let cb represent a horizontal line and ab a vertical line of equal length; draw the diagonal ac; the angle acb will be one of 45 °; let d be the middle point of the vertical line ab. Then the semi-parabola dc is the one which is determined by the sublimity ad and the altitude db, while its terminal speed at c is that which would be acquired at b by a particle falling from rest at a. If now ag be drawn parallel to bc, the sum of the altitude and sublimity for any other semi-parabola having the same terminal speed will, in the manner explained, be equal to the distance between the parallel lines ag, and bc. Moreover, since (282) it has already been shown that the amplitudes of two semi-parabolas are the same when their angles of elevation differ from 45° by like amounts it follows that the same computation which is employed for the larger elevation will serve also for the smaller. Let us also assume 10000 as the greatest amplitude for a parabola whose angle of elevation is 45°; this then will be the length of the line ba and the amplitude of the semi-parabola bc. This number, 10000, is selected because in these calculations we employ a table of tangents in which this is the value of the tangent of 45°. And now, coming down to business, draw the straight line ce making an acute angle ecb greater than acb: the problem now is to draw the semi-parabola to which the line ec is a tangent and for which the sum of the sublimity and the altitude is the distance ba. Take the length of the tangent^* be from the table of tangents, using the angle bce as an argument: let f be the middle point of be; next find a third proportional to bf and bi (the half of bc), which is of necessity greater than fa. ^** Call this fo. We have now discovered that, for the parabola inscribed 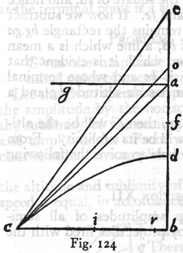[302] in the triangle ecb having the tangent ce and the amplitude cb, the altitude is bf and the sublimity fo. But the total length of bo exceeds the distance between the parallels ag and cb, while our problem was to keep it equal to this distance: for both the parabola sought and the parabola dc are described (283) by projectiles fired from c with the same speed. Now since an infinite number of greater and smaller parabolas, similar to each other, may be described within the angle bce we must find another parabola which like cd has for the sum of its altitude and sublimity the height ba, equal to bc.

Therefore lay off cf so that, ob:ba = bc:cr; then cr will be the amplitude of a semi-parabola for which bce is the angle of elevation and for which the sum of the altitude and sublimity is the distance between the parallels ga and cb, as desired. The process is therefore as follows: One draws the tangent of the given angle bce; takes half of this tangent, and adds to it the quantity, fo, which is a third proportional to the half of this tangent and the half of bc; the desired amplitude cr is then found from the following proportion ob:ba = bc:cr. For example let the angle ecb be one of 50° its tangent is 11918, half of which, namely bf, is 5959; half of bc is 5000; the third proportional of these halves is 4195, which added to bf gives the value 10154 for bo. Further, as ob is to ab, that is, as 10154 is to 10000, so is bc, or 10000 (each being the tangent of 45°) to cr, which is the amplitude sought and which has the value 9848, the maximum amplitude being bc, or 10000. The amplitudes of the entire parabolas are double these, namely, 19696 and 20000. This is also the amplitude of a parabola whose angle of elevation is 40°, since it deviates by an equal amount from on of 45°. [303]

SAGR. In order to thoroughly understand this demonstration I need to be shown how the third proportional of bf and bi is, as the Author indicates, necessarily greater than fa.

SALV. This result can, I think, be obtained as follows. The square of teh mean proportional between two lines is equal to the rectangle formed by these two lines. Therefore the square of bi (or of bd which is equal to be) must be equal tot he rectangle formed by fb and the desired third proportional. This third proportional is necessarily greater than fa because the rectangle formed by bf and fa is less than the square of bd by an amount equal to the square of df, as shown in Euclid, II. I. Besides it is to be observed that the point f, which is the middle point of the (284) tangent eb, falls in general above a and only once at a; in which cases it is self-evident that the third proportional to the half of the tangent and to the sublimity be lies wholly above a. But the Author has taken a case where it is not evident that the third proportional is always greater than fa, so that when laid off above the point f it extends beyond the parallel ag.

Now let us proceed. It will be worth while, by the use of this table, to compute another giving the altitudes of these semi-parabolas described by projecti8les having the same initial speed. The construction is as follows: [304]

(285)

[305]

PROBLEM. PROPOSITION XIII

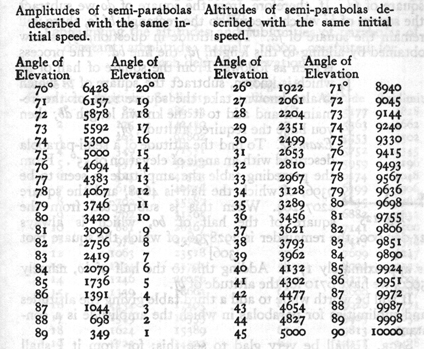
From the amplitudes of semi-parabolas given in the preceding table to find the altitudes of each of the parabolas described with the same initial speed.

Let bc denote the given amplitude; and let ob, the sum of the altitude and sublimity, be the measure of the initial speed which is understood to remain constant. Next we must find and determine the altitude, which we shall accomplish by so dividing ob that the rectangle contained by its parts shall be equal to the square of half the amplitude, bc. Let f denote this point of division and d and i be the middle points of ob and bc respectively. The square of ib is dqual to the rectangle bf. fo; but the square of do is equal to the sum of the rectangle bf. fo and the (286) square of fd. If, therefore, from the square of do we subtract the square of be which is equal to the rectangle bf. fo, there will remain the square of fd. The altitude in question, bf, is now obtained by adding to this length, fd, the line bd. The process is then as follows: From the square of half of bo which is known, subtract the square of be which is also known; take the square root of the remainder and add to it the known length db; then you have the required altitude, bf.

Example. To find the altitude of a semi-parabola described with an angle of elevation of 55°. From the preceding table the amplitude is seen to be 9396, of which the half is 4698, and the square 22071204. When this is subtrancted from the square of the half of bo, which is always 25,000,000, the remaineder is 2928796, of which the square root [306] is approximately 1710. Adding this to the half of bo, namely 5000, we have 6710 for the altitude of bf.

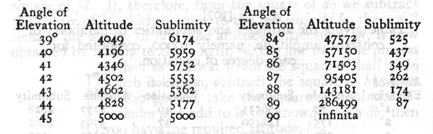
It will be worth while to add a third table giving the altitudes and sublimities for parabolas in which the amplitude is a constant.

SAGR. I shall be very glad to see this; for from it I shall learn the difference of speed and force [degl'impeti e delle forze] required to fire projectiles over the same range with what we call mortar shots. This difference will, I believe, vary greatly with the elevation so that it, for example, one wished to employ an elevation of 3° or 4°, or 87° or 88° and yet give the ball the same range which it had with an elevation of 45° (where we have shown the initial speed to be a minimum) the excess of force required will, I think, be very great.

SALV. You are quite right, sir; and you will find that in order to perform this operation completely, at all angles of elevation, you will have to make great strides toward an infinite speed. We pass now to the consideration of the table.

(287) [307]

(288)

[308]

PROPOSITION XIV

To find for each degree of elevation the altitudes and sublimities of parabolas of constant amplitude.

The problem is easily solved. For if we assume a constant amplitude of 10000, then half the tangent at any angle of elevation will be the altitude. Thus, to illustrate, a parabola having an angle of elevation of 30° and an amplitude of 10000, will have an altitude of 2887, which is approximately one-half the tangent. And now the altitude having been found, the sublimity is derived as follows. Since it has been proved that half the amplitude of a semi-parabola is the mean proportional between the altitude and sublimity, and since the altitude has already been found, and since the semi-amplitude is a constant, namely 5000, it follows that if we divide the square of the semi-amplitude by the altitude we shall obtain the sublimity sought. Thus in our example the altitude was found to be 2887; the square of 5000 is 25,000,000, which divided by 2887 gives the approximate value of the sublimity, namely 8659.

SALV. Here we see, first of all, how very true is the statement made above, that, for different angles of elevation, the greater the deviation from the mean, whether above or below, the greater the initial speed [impeto e violenza] required to carry the projectile over the same range. For since the speed is the resultant of two motions, namely, one horizontal and uniform, the other vertical and naturally accelerated; and since the sum of the altitude and sublimity represents this speed, it is seen from the preceding table that this sum is a (289) minimum for an elevation of 45° where the altitude and sublimity are equal, namely, each 5000; and their sum 10000. But if we choose a greater elevation, say 50°, we shall find the altitude 5959, and the sublimity 4196, giving a sum of 10155; in like manner we shall find that this is precisely the value of the speed at 40° elevation, both angles deviating equally from the mean.

Secondly it is to be noted that, while equal speeds are required for each of two elevations that are equidistant from the mean, there is this curious alternation, namely, that the altitude and sublimity at the greater elevation correspond inversely to the sublimity and altitude at teh lower elevation. Thus in the [309] preceding example an elevation of 50° gives an altitude of 5959 and a sublimity of 4196; while an elevation of 40° corresponds to an altitude of 4196 and a sublimity of 5959. And this holds true in general; but it is to be remembered that, in order to escape tedious calculations, no account has been taken of fractions which are of little moment in comparison with such large numbers.

SAGR. I note also in regard to the two components of the initial speed [impeto] that the higher the shot the less is the horizontal and the greater the vertical component; on the other hand, at lower elevations where the shot reaches only a small height the horizontal component of the initial speed must be great. In the case of a projectile fired at an elevation of 90°, I quite understand that all the force [forza] in the world would not be sufficient to make it deviate a single finger's breadth from the perpendicular and that it would necessarily fall back into its initial position; but in the case of zero elevation, when the shot is fired horizontally, I am not so certain that some force, less than infinite, would not carry the projectile some distance; thus not even a cannon can fire a shot in a perfectly horizontal direction, or as we say, point blank, that is, with no elevation at all. Here I admit there is some room for doubt. The fact I do not deny outright, because of another phenomenon apparently no less remarkable, but yet one for which I have conclusive evidence. This phenomenon is the impossibility of stretching (290) a rope in such a way that it shall be at once straight and parallel to the horizon; the fact is that the cord always sags and bends and that no force is ssufficient to stretch it perfectly straight.

SALV. In this case of the rope than, Sagredo, you cease to wonder at the phenomenon because you have its demonstration; but if we consider it with more care we may possibly discover some correspondence between the case of the gun and that of the string. The curvature of the path of the shot fired horizontally appears to result from two forces, one (that of the weapon) drives it horizontally and the other (its own weight)draws it vertically downward. So in stretching the rope you have the force which pulls it horizontally and its own weight which acts downwards. The circumstances in these two cases are, therefore, very similar. If then you attribute to the weight of the rope a power and [310] energy [possanza ed energia] sufficient to oppose and overcome any stretching force, no matter how great, why deny this power to the bullet?

Besides I must tell you something which will both surprixe and please you, namely, that a cord stretched more or less tightly assumes a curve which closely approximates the parabola. This similarity is clearly seen if you draw a parabolic curve on a vertical plane and then invert it so that the apex will lie at the bottom and the base remain horizontal; for, on hanging a chain below the base, you will observe that, on slackening the chain more or less, it bends and fits itself to the parabola; and the coincidence is more exact in proportion as the parabola is drawn with less curvature or, so to speak, more stretched; so that using parabolas described with elevations less than 45° the chain fits its parabola almost perfectly.

SAGR. Then with a fine chain one would be able to quickly draw many parabolic lines upon a plane surface.

SALV. Certainly and with no small advantage as I shall show you later.

SIMP. But before going further, I am anxious to be convinced at least of that proposition of which you say that there is a (291) rigid demonstration; I refer to the statement that it is impossible by any force whatever to stretch a cord so that it will lie perfectly straight and horizontal.

SAGR. I will see if I can recall the demonstration; but in order to understand it, Simplicio, it will be necessary for you to take for granted concerning machines hwat is evident not alone from experiment but also from theoretical considerations, namely, that the velocity of a moving body [velocità del movente], even when its force [forza] is small, can overcome a very great resistance exerted by a slowly moving body, whenever the velocity of the moving body bears to that of the reisiting body a greater ratio than the resistance [resistenza] of the resisting body to the force [forza] of the moving body.

SIMP. This I know very well for it has been demonstrated by Aristotle in his Questions in Mechanics; it is also clearly seen in the lever and the steelyard where a counterpoise weighing not more than 4 poinds will lift a weight of 400 provided that the distance of the counterpoise from the axis about which the steelyard rotates be more than one hundred times as great as the distance between this axis and the point of support for [311] the large weight. This is true because the counterpoise in its descent traverses a space more than one hundred times as great as that moved over by the large weight in the same time; in other words tha small counterpoise moves with a velocity which is more than one hundred times as great as that of the large weight.

SAGR. You are quite right; you do not hesitate to admit that however small the force [forza] of the moving body it will overcome any resistance, however great, provided it gains more in velocity than it loses in force and weight [vigore e gravità]. Now let us return to the case of the cord. In the accompanying figure ab represents a line passing through two fixed poins a and b; at the extremities of this line hang, as you see, two large weights c and d, which stretch it with great force and keep it truly straight, seeing that it is merely a line without weight. Now I wish to remark that if from the middle point of this line, (292) which we may call e, you suspend any small weight, say h, the line ab will yield toward the point f and on account of its elangation will compel the two heavy weights c and d to rise. This I shall demonstrate as follows: with the points a and b as centers describe the two quadrants, eig and elm; now since the two semi-diameters ai and bl are dqual to ae and eb, the remainders fi and fl are the excesses of the lines af and fb over ae and eb; they therefore determine the rise of the weights as c and d, assuming of course that the weight h has taken the position f. But the weight h 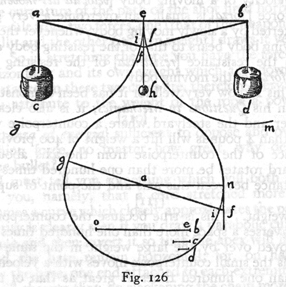[312] will take the position f, whenever the line ef which represents the descent of h bears to the line fi -- that is, to the rise of the weights c and d -- a ratio which is greater than the ratio of the weight of the two large bodies to that of the body h. Even when the weights of c and d are very great and that of h very small this will happen; for the excess of the weights c and d over the weight of h can never be so great but that the excess of the tangent ef over the segment fi may be proportionally greater. This may (293) be proved as follows: Draw a circle of diameter gai; draw the line bo such that the ratio of its length to another length c, c > d, is the same as the ratio of the weights c and d to the weight h. Since c > d, the ratio fo bo to d is greater than that of bo to c. Take be a third propotional to ob and d; prolong the diameter gi to a point f such that gi:if = oe:eb; and from the point f draw the tangent fn; then since we already have oe:eb = gi:if, we shall obtain, by compounding ratios, ob:eb = gf:if. But d is a mean proportional between ob and be; while nf is a mean proportional between gf and fi. Hence nf bears to fi the same ratio as that of cb to d, which is greater than that of the weights c and d to the weight h. Since then the descent, or velocity, of teh weight h bears to the rise, or velocity, of the weights c and d a greater ratio than the weight of the bodies c and d bears to the weight of h, it is clear that the weight h will descend and the line ab will cease to be straight and horizontal.

And now this which happens in the case of a weightless cord ab when any small weight h is attached at the point e, happens also when the cord is made of ponderable matter but without any attached weight; because in this case the material of which the cord is composed functions as a suspended weight.

SIMP. I am fully satisfied. So now Salviati can explain, as he jpromised, the advantage of such a chain and, afterwards, present the speculations of our Academician on the subject of impulsive forces [forza della percossa].

SALV. Let the preceding discussions suffice for to-day; the hour is already late and the time remaining will not permit us to clear up the subjects proposed; we may therefore postpone our meeting until another and more opportune occasion.

SAGR. I concur in your opinion, because after various conversations with intimate friends of our Academician I have concluded that this question of impulsive forces is very obscure, and I think that, up to the present, none of those who have treated [313] this subject have been able to clear up its dark corners which lie almost beyond the reach of human imagination; among the various views which I have heard expressed one, strangely fantastic, (294) remains in my memory, namely, that impulsive forces are indeterminate, if not infinite. Let us, therefore, await the convenience of Salviati. Meanwhile tell me what is this which follows the discussion of projectiles.

SALV. These are some theorems pertaining to the centers of gravity of solids, discovered by our Academician in his youth, and undertaken by him because he considered the treatment of Federigo Comandino to be somewhat incomplete. The propositions which you have before you would, he thought, meet the deficiencies of Comandino's book. The investigation was undertaken at the instance of the Illustrious Marquis Guid'Ubaldo Dal Monte, a very distinguished mathematician of his day, as is evidenced by his various publications. To this gentleman our Academician gave a copy of this work, hoping to extend the investigation to other solids not treated by Comandino. But a little later there chanced to fall into his hands the book of the great geometrician, Luca Valerio, where he found the subject treated so completely that he left off his own investigations, although the methods which he employed were quite different from those of Valerio.

SAGR. Please be good enough to leave this volume with me until our next meeting so that I may be able to read and study these proposition in the order in which they are written.

SALV. It is a pleasure to comply with your request and I only hope that the propositions will be of deep interest to you.

END OF THE FOURTH DAY. (295)

APPENDIX

Containing some theorems, and their proofs, dealing with centers of gravity of solid bodies, written by the same Author at an earlier date. ^*

[FINIS]

index previous next (footnotes)