62  Special Relativity: Kinematics

    Michael Fowler, UVa

A Quicker Derivation of the Lorentz Transformations

 The Modern Physics lectures you just reviewed (I hope), presented a derivation of the Lorentz transformations between two parallel frames $S,S^{\prime }$ with $S^{\prime }$ moving at constant speed $v$ along the common $x$ axis relative to $S,$ both taking the zero of time to be when the origins coincide. We followed Einstein’s thought experiments, all based on the assumption that the speed of light is the same in all inertial frames.

We’ll now show how, assuming the invariance of the speed of light, and that the equations are linear (like the Galilean ones), and that the time as observed on a receding clock doesn’t depend on the direction in which the clock is receding, we can derive the equations quite easily.

The Lorentz transformations relate the coordinates $\left(ct,x,y,z\right)$ of an event in one inertial frame $S$ to those $\left(c{t}^{\prime },x^{\prime },y^{\prime },z^{\prime }\right)$ in another inertial frame $S^{\prime }.$ We’ll take the corresponding axes in the two frames to be parallel, and the relative frame velocity to be along the $x$ -axis.  And, we’ll write the time coordinate as $ct$ so all coordinates have the same dimension. (This must be so, of course,  but often units with $c=1$ are chosen, so it’s not always apparent. Or, as in some GR books, time is measured in meters.)

Taking the frame origins to coincide at $t=t^{\prime }=0,$ the origin $O^{\prime }$ in $S^{\prime }$ must therefore correspond to $x=vt$ in $S$. 

Let’s now assume that the transformation from $\left(ct,x\right)$ to $\left(c{t}^{\prime },x^{\prime }\right)$ is linear (and we’ll assume $y,z$ are unchanged).  Then we can write:

$\left(\begin{array}{c}c{t}^{\prime }\\ x^{\prime }\end{array}\right)=\left(\begin{array}{cc}\alpha & \beta \\ \gamma & \delta \end{array}\right)\left(\begin{array}{c}ct\\ x\end{array}\right).$

Imagine now the path of a flash of light emitted at the origin at the instant the two origins coincided.  A flash moving in the positive direction is given by $x=ct$ and also by $x^{\prime }=c{t}^{\prime }$, so one must imply the other.  Putting this in the equation gives $\alpha +\beta =\gamma +\delta$. Now consider the flash moving in the negative direction, $-x=t,-x^{\prime }=t^{\prime }$: this gives $\alpha -\beta =\delta -\gamma$.   Putting these equations together we find:

$\left(\begin{array}{c}c{t}^{\prime }\\ x^{\prime }\end{array}\right)=\left(\begin{array}{cc}\alpha & \beta \\ \beta & \alpha \end{array}\right)\left(\begin{array}{c}ct\\ x\end{array}\right).$

Next, remembering that the origin $x^{\prime }=0$ in $S^{\prime }$ corresponds to $x=vt$ in $S$, and since $x^{\prime }=\beta ct+\alpha x$, it follows that $\beta c=-v\alpha$,

$\left(\begin{array}{c}c{t}^{\prime }\\ x^{\prime }\end{array}\right)=\left(\begin{array}{cc}\alpha & -v\alpha /c\\ -v\alpha /c& \alpha \end{array}\right)\left(\begin{array}{c}ct\\ x\end{array}\right).$

Imagine now a clock at the origin in $S$. The time $t^{\prime }=\alpha t$ observed on that clock from the moving frame $S^{\prime }$ cannot depend on the sign of the relative velocity, so $\alpha \left(-v\right)=\alpha \left(v\right)$, and therefore the inverse of the above transformation must have the same form (the same $\alpha$ ) with only the sign of $v$ changed.  Now, performing a transformation to a frame moving at $v$, then one to $-v,$  gets you back to the original frame:

$\left(\begin{array}{cc}\alpha & v\alpha /c\\ v\alpha /c& \alpha \end{array}\right)\left(\begin{array}{cc}\alpha & -v\alpha /c\\ -v\alpha /c& \alpha \end{array}\right)=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)$

from which $\alpha =1/\sqrt{1-v^2/c^2}$ and the Lorentz transformations follow:

$$\begin{array}{l}{t}^{\prime }=\frac{t-vx/c^2}{\sqrt{1-v^2/c^2}}\\ x^{\prime }=\frac{x-vt}{\sqrt{1-v^2/c^2}}\\ y^{\prime }=y\\ z^{\prime }=z.\end{array}$$

Standard Relativistic Notation

An "event" has four coordinates: position in three-dimensional space, plus time. That is, it's just a point in four-dimensional space, a.k.a. space time.  The standard notation is

$$\left(ct,x,y,z\right)\equiv \left(x^0,x^1,x^2,x^3\right),$$

Note that, for this position vector, we write “up” indices. 

It’s also standard notation to write:

$$\gamma =1/\sqrt{1-{\left(v/c\right)}^2},\overrightarrow{\beta }=\left(\overrightarrow{v}/c\right),c=1.$$

  (But we ‘ll be bilingual, sometimes using the old notation for simple arguments and concepts.)

Matrix Form of the Lorentz Transformation

The Lorentz transformation equations from frame $S^{\prime },$ moving at $v$ in the $x$-direction relative to $S,$ which we just derived in the preceding section, can be written in the new notation as:

$\left(\begin{array}{c}{x}^0\\ x^1\\ x^2\\ x^3\end{array}\right)=\left(\begin{array}{cccc}\gamma & \beta \gamma & 0& 0\\ \beta \gamma & \gamma & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)\left(\begin{array}{c}{x}^{0^{\prime }}\\ x^{1^{\prime }}\\ x^{2^{\prime }}\\ x^{3^{\prime }}\end{array}\right),$ 

But now we make a further change in notation: this is a Lorentz transformation, so we call the matrix $\Lambda$ (the Greek L for Lorentz), and furthermore, following Einstein, we write an element of the matrix as ${\Lambda }^{\alpha }{}_{\beta },$ so the equation above becomes

$$x^{\alpha }={\Lambda }^{\alpha }{}_{{\beta }^{\prime }}{x}^{{\beta }^{\prime }}.$$

You’ve probably come across Einstein’s dummy suffix notation, in which a suffix that appears twice is automatically summed over all its allowed values. In relativity, there is a further refinement: the suffix must appear once up, and once down, meaning that in writing the matrix the second suffix must be down for the summation rules to yield ordinary matrix multiplication when operating on a position vector.

(Hint:  to check the sign, take the nonrelativistic limit, $x^1=\beta \gamma x^{0^{\prime }}+\gamma x^{1^{\prime }}\cong vt+x^{\prime }.$ )

We see from the equation that

$${\Lambda }^{\alpha }{}_{{\beta }^{\prime }}=\frac{\partial x^{\alpha }}{\partial x^{{\beta }^{\prime }}},$$

noting that the “down” matrix index corresponds to an “up” index in the denominator.

Contravariant and Covariant Vectors

A contravariant vector is a set of four numbers in any inertial frame, $\overrightarrow{A}\underset{S}{\to }\left\{A^{\alpha }\right\}$, that transform from one frame to another like the coordinates of an event $\left\{x^{\alpha }\right\}:$ that is,

$$A^{\alpha }={\Lambda }^{\alpha }{}_{{\beta }^{\prime }}{A}^{{\beta }^{\prime }}.$$

Trivia: Why is it called contravariant? Historically, the fundamental transformation was of the basis axes. If the scale on the basis axes is doubled, say, then a vector (regarded as having an independent existence) will have its measured components halved$—$this is the “contra”.

Since we’ll soon be returning to electromagnetism, obviously we need to think about Maxwell’s equations in this new notation, and the first step is to see how differential operators $\partial /\partial x^{\nu }$ transform between frames.  More notation: we’ll sometimes write

$$\frac{\partial }{\partial x^{\nu }}={\partial }_{\nu }.$$

In fact, the frame transformation for differentials is simple: from the chain rule of differentiation

$\frac{\partial }{\partial x^{{\mu }^{\prime }}}=\frac{\partial \text{}{x}^{\nu }}{\partial \text{}{x}^{{\mu }^{\prime }}}\frac{\partial }{\partial \text{}{x}^{\nu }},$ 

we have

$${\partial }_{{\mu }^{\prime }}={\partial }_{\nu }{\Lambda }^{\nu }{}_{{\mu }^{\prime }}.$$

Four-vectors that transform in this way, $B_{{\mu }^{\prime }}=B_{\nu }{\Lambda }^{\nu }{}_{{\mu }^{\prime }},$ are called covariant vectors. Note that they have down indices. (As we’ll explain in a moment, this can also be written $B_{{\mu }^{\prime }}={\Lambda }_{{\mu }^{\prime }}{}^{\nu }{B}_{\nu },$ be careful with those indices!)

In ordinary three-dimensional space, regarding the contravariant vectors as column vectors, the covariant vectors are row vectors, and the matrix operates on them from the right. They are commonly called dual vectors, and in GR parlance they are often called forms. 

Important: The dot product of a contravariant vector and a covariant vector is invariant in a Lorentz transformation:

$$B_{{\mu }^{\prime }}{A}^{{\mu }^{\prime }}=B_{\nu }{\Lambda }^{\nu }{}_{{\mu }^{\prime }}{\Lambda }^{{\mu }^{\prime }}{}_{\sigma }{A}^{\sigma }=B_{\nu }{A}^{\nu },$$

 because

${\Lambda }^{\nu }{}_{{\mu }^{\prime }}{\Lambda }^{{\mu }^{\prime }}{}_{\sigma }=\frac{\partial \text{}{x}^{\nu }}{\partial \text{}{x}^{{\mu }^{\prime }}}\frac{\partial \text{}{x}^{{\mu }^{\prime }}}{\partial \text{}{x}^{\sigma }}=\text{}\frac{\partial \text{}{x}^{\nu }}{\partial \text{}{x}^{\sigma }}={\delta }_{\sigma }^{\nu },$ 

where ${\delta }_{\sigma }^{\nu }$ is the usual Kronecker delta in four dimensions, ${\delta }_{\sigma }^{\nu }=1$ if $\nu =\sigma ,$ zero otherwise.

${\Lambda }^{{\mu }^{\prime }}{}_{\nu }=\frac{\partial \text{}{x}^{{\mu }^{\prime }}}{\partial \text{}{x}^{\nu }},{\left({\Lambda }^{{\mu }^{\prime }}{}_{\nu }\right)}^{-1}={\Lambda }_{{\mu }^{\prime }}{}^{\nu }=\frac{\partial \text{}{x}^{\nu }}{\partial \text{}{x}^{{\mu }^{\prime }}}.$ 

Notice how important it is to be clear about which index is up and which down!

So we have these two different transformation rules: the contravariant one, a transformation with the same matrix as event coordinates,  $d\text{}\text{}{x}^{{\mu }^{\prime }}={\Lambda }^{{\mu }^{\prime }}{}_{\nu }d{x}^{\nu },$  and what is called the covariant one, having the same matrix as the differential operator set, $\frac{\partial }{\partial x^{{\mu }^{\prime }}}={\Lambda }_{{\mu }^{\prime }}{}^{\nu }\frac{\partial }{\partial x^{\nu }}.$   This last equation is usually written

$${\partial }_{{\mu }^{\prime }}={\Lambda }_{{\mu }^{\prime }}{}^{\nu }{\partial }_{\nu },$$

and any set of four numbers defined in each frame that transforms like this is called a covariant vector (and has down indices).

Since ${\Lambda }^{\mu }{}_{\nu },{\Lambda }_{\mu }{}^{\nu }$ are inverses of each other, a product of a covariant and a contravariant vector is invariant:

$A^{{\mu }^{\prime }}{B}_{{\mu }^{\prime }}={\Lambda }^{{\mu }^{\prime }}{}_{\nu }{\Lambda }_{{\mu }^{\prime }}{}^{\sigma }{A}^{\nu }{B}_{\sigma }={\delta }_{\nu }^{\sigma }{A}^{\nu }{B}_{\sigma }=A^{\sigma }{B}_{\sigma }.$ 

The Metric Tensor.  Magnitude of a Vector

Exercise:  check that under a Lorentz transformation, ${\overrightarrow{x}}^2-c^2{t}^2$ is invariant.  In fact, this quantity is called the magnitude of the four-vector.  Unlike most magnitudes, this one can be negative, or zero, for a nonzero vector.  To write it in terms of the new notation, we have to "square" the vector $x^{\mu },$ remembering that the time and space contributions have opposite signs.

The way this is done is to introduce a metric tensor,

$g_{\mu \nu }=\left(\begin{array}{cccc}-1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right).$ 

(Some authors, including Jackson, have an overall minus sign! See the discussion below.)

With this, the position vector $\left(x^0,x^1,x^2,x^3\right)$ can be converted to one with down indices by:

$x_{\mu }=g_{\mu \nu }{x}^{\nu },$ 

and we see this gives $\left(x_0,x_1,x_2,x_3\right)=\left(-x^0,x^1,x^2,x^3\right).$ 

(The index can be raised with $g^{\mu \nu },$ which is the inverse of $g_{\mu \nu },$ except that in our special relativity case, they're the same.)

The magnitude of the vector is written

$x^{\mu }{x}_{\mu }=g_{\mu \nu }{x}^{\mu }{x}^{\nu }={\overrightarrow{x}}^2-c^2{t}^2.$ 

Incidentally, we can see from the Lorentz transformation above why the matrix ${\Lambda }^{\mu }{}_{\nu }$ is the inverse of ${\Lambda }_{\mu }{}^{\nu }.$ Lowering the first index changes the signs of elements ${\Lambda }_0{}^0,{\Lambda }_0{}^1,{\Lambda }_0{}^2,{\Lambda }_0{}^3,$ lowering the second index changes the signs of ${\Lambda }_0{}^0,{\Lambda }_1{}^0,{\Lambda }_2{}^0,{\Lambda }_3{}^0,$ the net result is to reverse the velocity.

The Interval

One more piece of jargon: the interval.  Since the Lorentz transformation is linear, and true for arbitrary space time points, the four-vector difference $\Delta x^{\mu }$ between two space time points clearly also transforms as a four vector, its magnitude is

$\begin{array}{c}d{s}^2=\Delta x^{\mu }\Delta x_{\mu }\\ =-{\left(\Delta x^0\right)}^2+{\left(\Delta x^1\right)}^2+{\left(\Delta x^2\right)}^2+{\left(\Delta x^3\right)}^2\\ =-c^2{\left(\Delta t\right)}^2+{\left(\Delta x\right)}^2+{\left(\Delta y\right)}^2+{\left(\Delta z\right)}^2,\end{array}$ 

and this "square", the so-called magnitude, rather than the vector itself, is called the interval.

Obviously, it can be positive, negative, or zero.

Warning: Sign of the Metric Tensor

We have chosen a diagonal metric tensor with elements -1, 1, 1, 1, so spacelike separated points have a positive interval separation. Unfortunately, an almost equally popular choice is 1, -1, -1, -1, sometimes called a timelike metric, and the one used by Jackson.  The spacelike metric is standard in General Relativity, the timelike more common in High Energy Physics.

Spacelike, Timelike, Lightlike

Two events $\left(c{t}_1,x_1,y_1,z_1\right)$, $\left(c{t}_2,x_2,y_2,z_2\right)$ are said to be spacelike separated if the interval between them $-c^2{\left(t_2-t_1\right)}^2+{\left(x_2-x_1\right)}^2+{\left(y_2-y_1\right)}^2+{\left(z_2-z_1\right)}^2=\Delta s^2>0.$ 

It is important to note that spacelike separation in one inertial frame of reference means spacelike separation in all inertial frames, since the magnitude is invariant under Lorentz transformation.

Similarly, timelike separation is $\Delta s^2<0$, lightlike separation $\Delta s^2=0$.

 Points lightlike separated from the origin are said to be on the light cone,

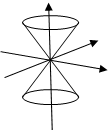which is really two cones having vertices at the origin, the forward (in time) light cone, and the backward light cone. A light signal sent from the origin (meaning $ct=x=0$ ) could trigger an event (a bomb?) anywhere on the forward light cone, a light signal from anywhere on the backward light cone could trigger an event at the origin.

An event at the origin cannot be the cause of another event which is outside the forward light cone.

Exercise:  Imagine two observers in inertial frames moving relative to each other. Each observer has light detectors placed throughout the frame. The origins coincide at $t=0,$ and at that moment a light flashes at the common origin. From the detectors, each observer will say that a spherical surface of light goes outwards, centered at that observer’s origin (and remember these origins are moving relative to each other). Explain why there is no contradiction here.   

Worldlines: As a particle moves through space time, the path traced is termed the worldline.  Since particles travel at less than the speed of light, the world line lies within the forward light cone.  A particle at rest has a worldline along the axis of the cone: in other words, the time axis.  A photon has a world line on the surface of the light cone.

Relativistic Addition of Velocities

Deriving the Equations

As stated above, $\left(c\Delta t,\Delta x,\Delta y,\Delta z\right)$ transforms just as $\left(ct,x,y,z\right)$ does, we'll write the transformation

$$\begin{array}{l}\Delta t=\gamma \left(\Delta t^{\prime }+v\Delta x^{\prime }/c^2\right)\\ \Delta x=\gamma \left(v\Delta t^{\prime }+\Delta x^{\prime }\right)\\ \Delta y=\Delta y^{\prime },\Delta z=\Delta z^{\prime }.\end{array}$$

From these equations in the limit of small displacements, $\Delta x/\Delta t$  gives the addition of velocities formulas

$$\frac{\Delta x}{\Delta t}=u_x=\frac{\Delta x^{\prime }+v\Delta t^{\prime }}{\Delta t^{\prime }+v\Delta x^{\prime }/c^2}=\frac{{u^{\prime }}_x+v}{1+{u^{\prime }}_{x}v/c^2}$$

and

$$u_y=\frac{{u^{\prime }}_y}{\gamma \left(1+{u^{\prime }}_{x}v/c^2\right)}.$$

(Recall the primed frame is moving at $v$ in the positive $x$-direction relative to the unprimed frame.)

Exercise:   Suppose a space station moving at $v$ in the $x$-direction relative to an observer sends a rocket ship forward at $u$ relative to the ship.  What is the velocity of the rocket ship relative to the “stationary” observer? 

Now suppose the space station is moving at 0.8c relative to the observer, the rocket ship moves at 0.8c relative to the space station, and the rocket ship fires a missile forward at 0.8c relative to itself. What is the speed of the missile relative to the original observer?

Rotations and Boosts, Rapidity

Notice now that the 4 x 4 Lorentz matrix can also represent ordinary rotations in the three-dimensional space:

$\left(\begin{array}{c}{x}^0\\ x^1\\ x^2\\ x^3\end{array}\right)=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& \cos \theta & \sin \theta & 0\\ 0& -\sin \theta & \cos \theta & 0\\ 0& 0& 0& 1\end{array}\right)\left(\begin{array}{c}{x}^{0^{\prime }}\\ x^{1^{\prime }}\\ x^{2^{\prime }}\\ x^{3^{\prime }}\end{array}\right),$ 

and manifestly $x^{\mu }{x}_{\mu }$ is invariant.  Any three-dimensional space rotation can be represented by the lower-right 3 X 3 minor of the full 4 X 4 matrix.

In fact, the Lorentz transformation to a moving frame$—$called a "boost"$—$can be formulated in a strikingly similar way, in terms of a variable much favored by high energy physicists, the rapidity $\psi ,$ defined by

$\frac{v}{c}=\beta =\tanh \psi ,\gamma =1/\sqrt{1-{\beta }^2}=\cosh \psi .$ 

  Rapidity proves to be a very useful parameter, because for one thing

$\tanh \left(\psi +{\psi }^{\prime }\right)=\frac{\tanh \psi +\tanh {\psi }^{\prime }}{1+\tanh \psi \tanh {\psi }^{\prime }}$ 

which is exactly the Lorentz addition formula for velocities!  (Recall $"u+v"=\frac{u+v}{1+uv/c^2}.$ )  This means that in successive boosts you just add the rapidities.

The Lorentz transformation for boosting from rest to a rapidity $\psi$ along the $x$-axis is:

$\left(\begin{array}{c}{x}^0\\ x^1\\ x^2\\ x^3\end{array}\right)=\left(\begin{array}{cccc}\cosh \psi & \sinh \psi & 0& 0\\ \sinh \psi & \cosh \psi & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)\left(\begin{array}{c}{x}^{0^{\prime }}\\ x^{1^{\prime }}\\ x^{2^{\prime }}\\ x^{3^{\prime }}\end{array}\right).$ 

That is, a particle at rest in the moving (boosted) frame is moving with rapidity $\psi$ in the original frame.

 Notice the similarity to the three-dimensional rotation!  The sign difference ensures both transformations are unitary.  Some authors (for instance, Zangwill) take time to be an imaginary variable, so the rotation and boost transformations look identical, but we'll stick with the more common practice.  (There are in fact deep mathematical differences between rotations and boosts, as we'll see.)

Lorentz Transformation for Arbitrary Direction

For a boost of $v$ in the $x$-direction the coordinates in the boosted frame are:

$\left(\begin{array}{c}{x}^{0^{\prime }}\\ x^{1^{\prime }}\\ x^{2^{\prime }}\\ x^{3^{\prime }}\end{array}\right)=\left(\begin{array}{cccc}\gamma & -\beta \gamma & 0& 0\\ -\beta \gamma & \gamma & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)\left(\begin{array}{c}{x}^0\\ x^1\\ x^2\\ x^3\end{array}\right)$

For a boost of $\overrightarrow{v}=\overrightarrow{\beta }c,$ the corresponding matrix $M$ is: $$

$\left(\begin{array}{c}{x}^{0^{\prime }}\\ x^{1^{\prime }}\\ x^{2^{\prime }}\\ x^{3^{\prime }}\end{array}\right)=\left[\begin{array}{cccc}\gamma & -{\beta }_1\gamma & -{\beta }_2\gamma & -{\beta }_3\gamma \\ -{\beta }_1\gamma & 1+(\gamma -1)\frac{{\beta }_1^2}{{\beta }^2}& (\gamma -1)\frac{{\beta }_1{\beta }_2}{{\beta }^2}& (\gamma -1)\frac{{\beta }_1{\beta }_3}{{\beta }^2}\\ -{\beta }_2\gamma & (\gamma -1)\frac{{\beta }_1{\beta }_2}{{\beta }^2}& 1+(\gamma -1)\frac{{\beta }_2^2}{{\beta }^2}& (\gamma -1)\frac{{\beta }_2{\beta }_3}{v^2}\\ -{\beta }_3\gamma & (\gamma -1)\frac{{\beta }_1{\beta }_3}{{\beta }^2}& (\gamma -1)\frac{{\beta }_2{\beta }_3}{{\beta }^2}& 1+(\gamma -1)\frac{{\beta }_3^2}{{\beta }^2}\end{array}\right]\left(\begin{array}{c}{x}^0\\ x^1\\ x^2\\ x^3\end{array}\right).$

Notice first that this does give the right answer for the boost along the $x$ -axis.

But how did we come up with this matrix $M?$ 

Our strategy for boosting in an arbitrary direction is to reorient the system so that that direction becomes the $x$ -axis, apply our known boost, then rotate it back.

To see how this works, we write the above matrix in terms of blocks, as follows (vectors in bold)

$\left(\begin{array}{cc}\gamma & -\gamma {𝜷}^T\\ -\gamma 𝜷& I+\left(\gamma -1\right)𝜷{𝜷}^T/{\beta }^2\end{array}\right)$.

In this same block notation, a three-dimensional rotation has the form

$$\left(\begin{array}{cc}1& 0\\ 0& R\end{array}\right)$$

and its inverse is  $\left(\begin{array}{cc}1& 0\\ 0& R^T\end{array}\right)$.   If we choose $R$ such that $R\beta$ points along the $x$ -axis, then

$\left(\begin{array}{cc}1& 0\\ 0& R\end{array}\right)\left(\begin{array}{cc}\gamma & -\gamma {𝜷}^T\\ -\gamma 𝜷& I+\left(\gamma -1\right)𝜷{𝜷}^T/{\beta }^2\end{array}\right)\left(\begin{array}{cc}1& 0\\ 0& R^T\end{array}\right)=\left(\begin{array}{cc}\gamma & -\gamma {𝜷}^T{R}^T\\ -\gamma R\beta & I+\left(\gamma -1\right)R\beta {𝜷}^T{R}^T/{\beta }^2\end{array}\right)$

where $R\beta =\left(\begin{array}{c}\beta \\ 0\\ 0\end{array}\right),{𝜷}^T{R}^T=\left(\begin{array}{ccc}\beta & 0& 0\end{array}\right),$  so, putting those in, that last fearsome-looking matrix is actually trivial, it’s just the boost along the $x$ -axis, as we want.

Exercise: By working out the matrix multiplication for a vector, $A^{\prime }=MA,$ taking $A$ in components parallel and perpendicular to the boost direction, prove that (Jackson page 526)

$$\begin{array}{l}{A^{\prime }}_0=\gamma \left(A_0-𝜷\cdot A\right)\\ {A^{\prime }}_{\parallel }=\gamma \left(A_{\parallel }-\beta A_0\right)\\ {A^{\prime }}_{\perp }=A_{\perp }.\end{array}$$

Actually this is confusing: the matrix $M$ as written above operates on up index vectors. These look like down indices, but Jackson adds a footnote saying there are really elements of an up index (contravariant) vector… (The only difference would be the sign of the velocity, you should always check by looking at the low velocity limit.)

A Bit of Group Theory

The Lorentz boosts along the $x$-axis formed an Abelian (commutative) group, just as the set of rotations in a plane do.  The rotations in a plane are a subgroup of the group of three-dimensional rotations, which is of course non-abelian.  What about the set of all Lorentz boosts?  It turns out that this is not a group. A product of two Lorentz boosts in different directions is not just a Lorentz boost in some combined direction, it also has some rotation.  (We shall see the importance of this when we discuss the Thomas precession.)  The Lorentz group is the group of boosts plus rotations. Unfortunately, we do not have time to present the relevant group theory in terms of generators, etc., here.

Proper Time and Four-Velocity

Consider a spaceship going from one planet to another, the planets might have quite different velocities, so the distance covered by the ship will be different in the two planet rest frames.  One thing that won't be different is the time elapsed as measured by the crew of the spaceship.  This is called the proper time of the spaceship, the clock is always with the ship.  (Strictly, we’re assuming here that all frames are inertial. Otherwise, we need GR.)

An increment of proper time is denoted by $d\tau .$ 

If the spaceship moves $\Delta x^{\mu }$ in time $d\tau ,$ this incremental displacement transforms as a Lorentz four-vector.  Therefore, so does

$U^{\mu }=\frac{d{x}^{\mu }}{d\tau }.$ 

The four-vector $U^{\mu }$ is called the four-velocity.  In the nonrelativistic limit it becomes $\left(c,v^i\right)$, the spatial part just the ordinary velocity, and $\tau \to t,x^0=ct.$  

Now $U^{\mu }{U}_{\mu }=\frac{d{x}^{\mu }d{x}_{\mu }}{{\left(d\tau \right)}^2},$ but $d{x}^{\mu }d{x}_{\mu }$ is just the interval, which has the same value in all frames, including the frame in the ship, where it is $-{\left(cd\tau \right)}^2,$ so

$U^{\mu }{U}_{\mu }=-c^2.$ 

In the rest frame, where the incremental movement along the world line $d{x}^{\mu }$ is purely in the time direction, and is just $cd\tau ,$ the four-velocity is $\left(c,0,0,0\right).$  

In general, it's $\left(\gamma c,\gamma v^1,\gamma v^2,\gamma v^3\right).$  (In relativity papers and books, these formulas usually appear with $c=1.$ )

Minkowski Diagrams: Axes and Scales in the Transformed Frame

Contrasting Ordinary Rotations and Lorentz Transformations

Obviously, for ordinary rotations in a plane, the change of axes and scales is trivial: the transformation is

$$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right),$$

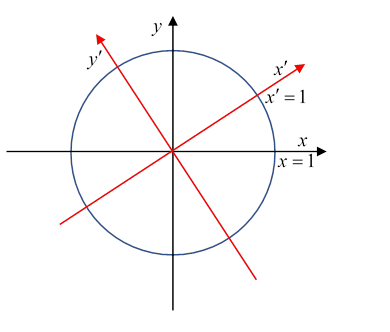
 the axes are rotated and the measuring scale doesn’t change: $x^{\prime }=1$ is where the new axis intersects the invariant unit circle

$$x^2+y^2=1.$$

On the other hand, for Lorentz transformations, things are a little more complicated:  instead of the simple invariant circles $x^2+y^2=R^2$, we evidently have invariant hyperbolae, $-c^2{t}^2+x^2=a^2$, or $-c^2{t}^2+x^2=-b^2$ ( $a,b$ real.)

The natural variable to describe these transformations is the rapidity $\psi ,$ so

$$\left(\begin{array}{c}c{t}^{\prime }\\ x^{\prime }\end{array}\right)=\left(\begin{array}{cc}\cosh \psi & -\sinh \psi \\ -\sinh \psi & \cosh \psi \end{array}\right)\left(\begin{array}{c}ct\\ x\end{array}\right)=\Lambda \left(\psi \right)\left(\begin{array}{c}ct\\ x\end{array}\right).$$

and of course ${\cosh }^2\psi -{\sinh }^2\psi =1$.

Recall that $\tanh \psi =0$ for $\psi =0,$ and $\tanh \psi \to \pm 1$ as $\psi \to \pm \infty .$ 

To see how the axes appear in the transformed frame, recall first that the lines $ct=\pm x$ must go to $c{t}^{\prime }=\pm x^{\prime }$, they constitute the two-dimensional version of the light cone.

This light cone invariance only works because there is one sign change in $\Lambda \left(\psi \right)$ compared with $R\left(\theta \right)$, (look at the matrices above).

That sign change means that under the transformation the $t^{\prime },x^{\prime }$ axes turn in opposite directions away from the original $t,x$ axes, so on going to larger and larger boosts, the axes close like scissors around the line $x=t$, never reaching it, of course.

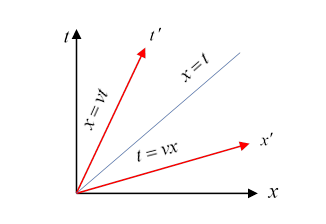
This is easy to see from the equations:  the $t$-axis is the line $x=0$, the $t^{\prime }$ axis is the line $x^{\prime }=0$, or $x=vt.$ 

Put another way: the $t$-axis is the “world line”, meaning the path in space time, of an object at rest at the origin in the original frame, the $t^{\prime }$-axis is the world line of an object at rest at the origin of the primed frame.

The $x^{\prime }$-axis is the line $t^{\prime }=0,$ so $t=vx$ in the original frame. 

So the primed frame axes are the original axes turned through opposite angles $\pm \theta$, $\tan \theta =v=\tanh \psi .$ This means that for small speeds, $\theta ,v,\psi$ are close, but as $\psi$ goes to infinity, $\theta$ just approaches 45°.

These diagrams, called Minkowski diagrams$—$first drawn by Minkowski a few years after Einstein published his special relativity paper. 

Finding Length and Time Scales in a New Frame:  Invariant Hyperbolae

We’ve now seen how the axes move, but we haven’t tracked what happens to the calibration$—$the scale on the axes. 

The way to do that is to use an invariant hyperbola, for example $-c^2{t}^2+x^2=1=-c^2{t^{\prime }}^2+{x^{\prime }}^2$.

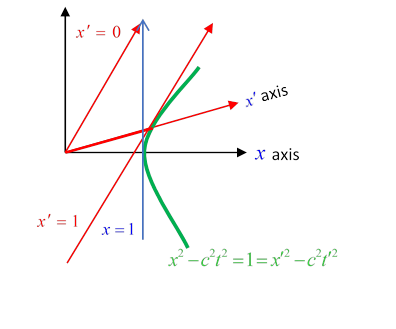
This hyperbola cuts the $x$ -axis at $x=1$, and the $x^{\prime }$ axis at $x^{\prime }=1.$ Note that $x^{\prime }=1$ is the tangent line to the unit hyperbola ${x^{\prime }}^2-c^2{t^{\prime }}^2=1$, it’s the minimum possible value of $x^{\prime }$ on that hyperbola.

Lorentz Contraction

Notice that from the diagram, in the $\left(x,ct\right)$ plane the point $x^{\prime }=1$ (on the hyperbola) is further from the origin than the point $x=1.$ Does this mean that a rod of unit length at rest in the primed frame (say, stretching from $x^{\prime }=0$ to $x^{\prime }=1$ ) will appear longer than unity in the $\left(x,ct\right)$ frame? 

Presumably not$—$that would be the opposite of Lorentz contraction.

So what’s going on?  The essential point is that we’re looking at the $x$-positions of the ends of the rod at different times $t.$ To measure the length of a moving rod, we obviously need to find the $x$-values of the end points at the same time $t$ --keep reading.

World Lines

As we mentioned earlier, the world line of a particle (or of a small part of a solid object) is its path in four-dimensional spacetime.

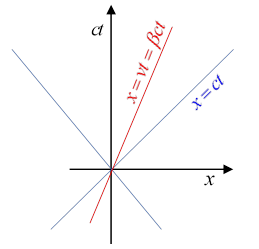
Here are some sample world lines in a two-dimensional subspace.  First, the light cone sections are world lines of photons, traveling at $c.$  A particle moving at constant velocity $x=vt$ is shown. The world line must be steeper than the light cone, since $v<c$. A particle at rest has a world line parallel to the $t$ axis, so the $t$ axis itself is the world line of a particle at rest at the origin.

Now, back to measuring the moving rod. We need to plot the world lines of the two ends, and find how far apart they are at, say, $t=0.$ Look back at the original diagram. The world line of the left end is just that of the primed origin, that is, it’s the $t^{\prime }$ axis, $x^{\prime }=0.$  The other end is moving at the same velocity, so its world line has the same slope: it’s $x^{\prime }=1,$ the tangent line to the unit hyperbola ${x^{\prime }}^2-c^2{t^{\prime }}^2=1$ ,as mentioned earlier.

Plotting the two world lines, we can see that their simultaneous intercepts on the axis are at points less than one unit apart.

Exercise:  check your understanding by using similar arguments to show that a rod of unit length at rest in the original unprimed frame will have length measured as less than one in the primed frame.

Time Dilation

We’ve just seen how an invariant space-like hyperbola can explain how each observer can see the other as Lorentz contracted. A time-like invariant hyperbola can show us that each sees the other’s clock as running slow.

Here the invariant hyperbola is $-c^2{t}^2+x^2=-1=-c^2{t^{\prime }}^2+{x^{\prime }}^2$:

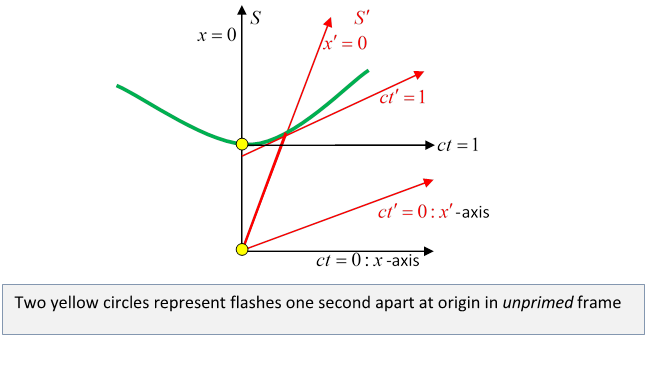
The red parallel lines here are the lines $c{t}^{\prime }=0$ and $c{t}^{\prime }=1$, both lines of simultaneity in the primed frame.

Suppose first that a clock in the unprimed frame flashes once a second.  The initial flash is seen by both observers to be at their common origin, $ct=c{t}^{\prime }=0$. The second flash, at $ct=1$, is clearly at $c{t}^{\prime }>1$ --the clock is running slow in the primed frame.

Now suppose a clock in the primed frame is flashing once a second.  As before, the initial flash is at the common origin. The next flash, at $c{t}^{\prime }=1,x^{\prime }=0$ is clearly at $ct>1:$

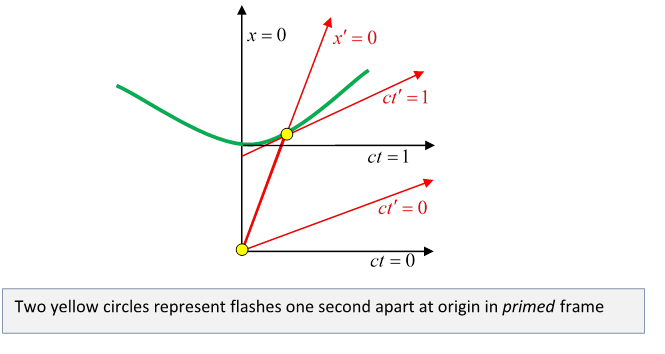
Look at the invariant hyperbolae and scale markings on this animation!

Four-Acceleration

The acceleration four vector is defined as $\overrightarrow{a}=d\overrightarrow{U}/d\tau$.  Notice that since the four velocity has constant magnitude $\overrightarrow{U}\cdot \overrightarrow{U}=-c^2,$ the four acceleration is always orthogonal to the four velocity: $\overrightarrow{U}\cdot d\overrightarrow{U}/d\tau =0$, and so in the frame of the moving object the four acceleration has only spatial components.

The acceleration four vector can also be written $a^{\alpha }=\frac{d{U}^{\alpha }}{d\tau }=\frac{d{U}^{\alpha }}{d{x}^{\beta }}\frac{d{x}^{\beta }}{d\tau }=U^{\beta }{\partial }_{\beta }{U}^{\alpha }$.

previous  index  next