64  Special Relativity: Electromagnetism

    Michael Fowler, UVa

(Like Griffiths, I follow Purcell.)

How Fields Transform

The whole point of using electric and magnetic fields is that if the electric field is defined in terms of the electrical force on a stationary charge, then it only depends on that local value $\overrightarrow{E}\left(\overrightarrow{r}\right),$ not on whether the field originated from another close-by point charge, or a distant larger one, or even a changing magnetic field.  An electric field is an electric field.

This means that to see how electric fields transform under Lorentz transformations, we can take the simplest possible way of producing the field, something easy to analyze in different frames.  The obvious candidate is a parallel plate capacitor, with infinite plates, a distance $d$ apart in their rest frame, having uniform surface charge density $\sigma .$ 

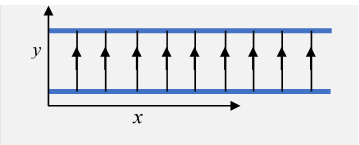
The electric field between the plates is $$\overrightarrow{E}=\frac{\sigma }{{\epsilon }_0}\widehat{\overrightarrow{y}}.$$  Suppose now the plates are in a frame $S^{\prime },$ and frame $S^{\prime }$ is moving in the $x$ -direction at speed $v$ relative to our lab frame $S.$ That is, the direction of motion is perpendicular to the direction of the field. 

Then from the Lorentz contraction of the plates, and the invariance of electric charge under a Lorentz transformation (we're assuming this, but it's extremely well-verified experimentally), the surface charge density increases by a factor $\gamma :$ 

$$\sigma \to {\sigma }^{\prime }=\frac{\sigma }{\sqrt{1-v^2/c^2}}=\gamma \sigma ,$$  and therefore so does the electric field strength:

${{\overrightarrow{E}}^{\prime }}_{\perp }=\gamma {\overrightarrow{E}}_{\perp }.$ 

The subscript $\perp$ is to make clear that this is the change in field strength in a transformation to a frame moving in a direction perpendicular to the field direction.

 How does motion in a direction parallel to the field affect it?  Not at all: the distance between the plates will shrink, but the plate surface charge density in unaffected, so the field doesn't change:

${{\overrightarrow{E}}^{\prime }}_{\parallel }={\overrightarrow{E}}_{\parallel }.$ 

Electric Field of a Point Charge in Uniform Motion

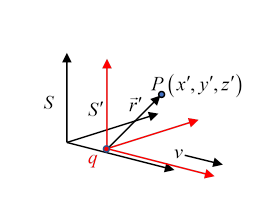
The equations above for ${\overrightarrow{E}}_{\perp },{\overrightarrow{E}}_{\parallel }$ give us enough information to construct the electric field of a moving point charge.  Let's assume the charge $q$ is at rest at the origin of the frame $S^{\prime },$ but that $S^{\prime }$ is moving to the right along the $x$ -axis at $v$ relative to the parallel lab frame $S.$ What does the electric field look like in $S$?  We know that in $S^{\prime },$ at the point $P$ with coordinates $\left(x^{\prime },y^{\prime },z^{\prime }\right)$ the field is

$${\overrightarrow{E}}^{\prime }=\frac{1}{4\pi {\epsilon }_0}\frac{q}{{r^{\prime }}^3}{\overrightarrow{r}}^{\prime }=\frac{1}{4\pi {\epsilon }_0}\frac{q}{{\left({x^{\prime }}^2+{y^{\prime }}^2+{z^{\prime }}^2\right)}^{3/2}}\left(x^{\prime },y^{\prime },z^{\prime }\right),$$ so in a frame $S$ moving relative to $S^{\prime }$ at velocity $-v$ along the $x$ axis, the $y,z$ components will be enhanced by a factor $\gamma ,$ the $x$ component won't change, so in frame $S$:

$${\overrightarrow{E}}_S=\frac{1}{4\pi {\epsilon }_0}\frac{q}{{\left({x^{\prime }}^2+{y^{\prime }}^2+{z^{\prime }}^2\right)}^{3/2}}\left(x^{\prime },\gamma y^{\prime },\gamma z^{\prime }\right).$$ The problem with this electric field in $S$ is that it's still written in $S^{\prime }$ coordinates!  Lorentz transforming to $S$ coordinates $\left(x,y,z\right)$ :

$\begin{array}{l}{x}^{\prime }=\gamma \left(x-vt\right)\\ y^{\prime }=y\\ z^{\prime }=z.\end{array}$ 

We now see that the electric field vector in the $S$ frame points in the direction $\gamma \left(x-vt,y,z\right).$ But in this frame $S$ at time $t$ the charge $q$ is at $\left(vt,0,0\right)$, so in fact the electric field at time $t$ is pointing directly away from the position of the charge at that instant!  (This should surprise you: remember that changes in an electric field caused by the source moving must propagate at the speed of light, not instantaneously: the space vector from the charge to the point where we're looking at the field is compressed in the $x$ direction by ${\gamma }^{-1},$ but the perpendicular component of the field is enhanced by $\gamma .$ )

So we've found the direction of the electric field of a steadily moving charge, but what about the magnitude of the field?  To find that, we need to put that denominator in the expression for ${\overrightarrow{E}}_S$ into $S$ frame coordinates.  Here it is:

$$\overrightarrow{E}=\frac{1}{4\pi {\epsilon }_0}\frac{\gamma q}{{\left({\gamma }^2{\left(x-vt\right)}^2+y^2+z^2\right)}^{3/2}}\left(x-vt,y,z\right).$$ Evidently, the field strength depends on direction.  It's useful to write the position vector of the point $P$ relative to the charge $q$ in the $S$ frame, $\left(x-vt,y,z\right)$, denoted by $\overrightarrow{R}$ in Griffiths, in spherical polar coordinates$—$all we really need is $\left(R,\theta \right)$ since the system has azimuthal symmetry about the direction of motion, and $x-vt=R\cos \theta ,\sqrt{y^2+z^2}=R\sin \theta ,$ so

$${\overrightarrow{E}}_S=\frac{1}{4\pi {\epsilon }_0}\frac{\gamma q\overrightarrow{R}}{{\left({\gamma }^2{R}^2{\cos }^2\theta +R^2{\sin }^2\theta \right)}^{3/2}}=\frac{1}{4\pi {\epsilon }_0}\frac{q\left(1-{\beta }^2\right)}{{\left(1-{\beta }^2{\sin }^2\theta \right)}^{3/2}}\cdot \frac{\overrightarrow{R}}{R^3}.$$

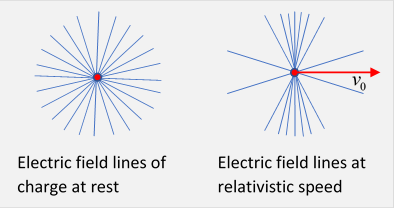
Notice that along the direction of motion, the electric field tends to zero as $\beta \to 1,$ $v\to c,$ but in the direction perpendicular to the path the field increases without limit. (It's always radial.)

What about equipotentials?  Since they always cut the radial field lines at right angles, don’t they have to be circular?  But the field strength varies with direction, so this gives a contradiction…?

Exercise:  figure this out.  Hint: What do you think “equipotential” means, say in the Coulomb gauge? The Lorenz gauge? How do equipotentials relate to the electric field here?

Electric and Magnetic Field Transformations

We showed at the beginning of this section that the electric field generated by uniformly charged plates in their rest frame, which in this section we'll label $S_0,$ led to a field stronger by a factor ${\gamma }_0$  on measuring it in a frame $S,$ where frame $S_0$ is moving at velocity $v_0$ (parallel to the plates) relative to $S.$ However, this is not the whole story$—$we looked at a special case, in which there was zero magnetic field in the first frame $S_0.$ In the general case, both electric and magnetic fields in one frame contribute to electric and magnetic fields in another.

To find the appropriate equations, we need to have an initial frame with both electric and magnetic fields.  It's not difficult: in the scenario we just discussed, there are both electric and magnetic fields in $S,$ because the now moving charged plates are also current sheets, generating a magnetic field between them. 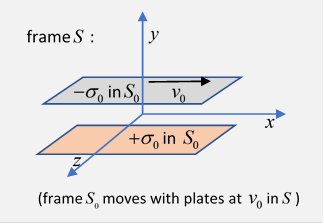So we just need to transform from this $S$ to another frame $\overline{S},$ let's have $\overline{S}$ moving at $v$ in the $x$ direction relative to $S.$ 

The plates $S_0,$ moving at $v_0$ in the $x$ direction relative to $S,$ constitute uniform current sheets, hence in $S$ there is a magnetic field between them (see figure) in the $z$ direction,  $B_z={\mu }_0\sigma v_0={\mu }_0{\gamma }_0{\sigma }_0{v}_0.$ 

So here the only nonzero components of the electric and magnetic fields in $S$ are $E_y,B_z.$

Now we're ready to transform to another frame $\overline{S}$ moving at $v$ in the $x$ direction relative to $S.$

To find how the fields transform, we just need to find the velocity ${\overline{v}}_0$ of the charged plates in $\overline{S},$ using the addition of velocities formula.

Since the plates are moving at $v_0$ in $S,$ and $\overline{S}$ is moving at $v$ in $S,$ in $\overline{S}$ the plates are moving at

$${\overline{v}}_0=\frac{v_0-v}{1-v_{0}v/c^2}.$$ Defining ${\overline{\gamma }}_0=1/\sqrt{1-{\overline{v}}_0^2/c^2},$ we have

$${\overline{\gamma }}_0=\frac{1}{\sqrt{1-\left(\frac{v_0-v}{1-v_{0}v/c^2}\right)}}=\frac{1-v_{0}v/c^2}{\sqrt{{\left(1-v_{0}v/c^2\right)}^2-{\left(v_0-v\right)}^2}}=\frac{1-v_{0}v/c^2}{\sqrt{1-v_0^2/c^2}\sqrt{1-v^2/c^2}}.$$ That is,

${\overline{\gamma }}_0=\left(1-v_{0}v/c^2\right){\gamma }_0\gamma .$ 

Hence the field transformation equations from $E_y,B_z$ in $S$ to ${\overline{E}}_y,{\overline{B}}_z$ in $\overline{S}$ are:

$$\begin{array}{c}{\overline{E}}_y={\overline{\gamma }}_0\frac{{\sigma }_0}{{\epsilon }_0}=\left(1-v_{0}v/c^2\right)\gamma {\gamma }_0\frac{{\sigma }_0}{{\epsilon }_0}\\ =\gamma \left(E_y-\frac{v}{c^2{\epsilon }_0{\mu }_0}{B}_z\right)=\gamma \left(E_y-v{B}_z\right).\end{array}$$ (Recall $B_z={\mu }_0\sigma v_0={\mu }_0\gamma {\sigma }_0{v}_0.$ )  Here $\gamma ,v$ refer to the relative velocities of $S,\overline{S}.$ 

For the magnetic field,

$$\begin{array}{c}{\overline{B}}_z={\mu }_0\overline{\gamma }{\sigma }_0{\overline{v}}_0={\mu }_0\left(1-v_{0}v/c^2\right)\gamma {\gamma }_0{\sigma }_o\frac{v_0-v}{1-v_{0}v/c^2}\\ ={\mu }_0\gamma {\gamma }_0{\sigma }_0\left(v_0-v\right)=\gamma \left(B_z-\left(v/c^2\right)E_z\right).\end{array}$$ Similarly, $E_z,B_y$ transform as follows under an $x$ direction boost:

$\begin{array}{l}{\overline{E}}_z=\gamma \left(E_z+v{B}_y\right),\\ {\overline{B}}_y=\gamma \left(B_y+\left(v/c^2\right)E_z\right).\end{array}$ 

We've already seen that under this $x$ direction boost

${\overline{E}}_x=E_x,$ 

To complete the picture,

${\overline{B}}_x=B_x.$ 

This is most simply proved by considering the magnetic field inside a long uniform solenoid,  in a frame moving  in the direction of its axis.  Lorentz contraction will increase the number of windings per unit length, but time dilation will decrease the current by the same factor.

Important Special Cases:

If $\overrightarrow{B}=0$ in $S,$ then $\overline{\overrightarrow{B}}=-\left(1/c^2\right)\overrightarrow{v}\times \overline{\overrightarrow{E}},$ 

If  $\overrightarrow{E}=0$ in $S,$ then $\overline{\overrightarrow{E}}=\overrightarrow{v}\times \overline{\overrightarrow{B}}.$ 

In particular, the magnetic field of a charge in uniform motion is

$$\overrightarrow{B}=\frac{{\mu }_0}{4\pi }\frac{qv\left(1-v^2/c^2\right)\sin \theta }{{\left(1-\left(v^2/c^2\right){\sin }^2\theta \right)}^{3/2}}\frac{\widehat{\overrightarrow{\varphi }}}{R^2}.$$ Exercise:  Sketch this for different values of the velocity. How does it relate to the field from a current?

previous  index  next