previous
index
next
How Classical Knowledge Reached Baghdad
Michael Fowler
The Classical Achievement in Mathematics and Science
With Ptolemy's Almagest giving detailed accounts and
predictions of the movement of the planets, we reach the end of the great classical
period in science. Let's review what was achieved.
First, the Babylonians developed a very efficient system of
numbers and measures of all kind, primarily for business purposes. Unfortunately,
it did not pass through to the Greeks and Romans, except for measures of time
and angle, presumably those are the units relevant for recording astronomical
observations. The Babylonians kept meticulous astronomical records over many
centuries, mainly for astrological purposes, but also to maintain and adjust
the calendar. They had tables of squares they used to aid multiplication, and
even recorded solutions to word problems which were a kind of pre-algebra, a
technique broadened and developed millennia later in Baghdad, as we shall see.
The Egyptians developed geometry for land measurement
(that's what it means!), the land being measured for tax assessment.
The Greeks, beginning with Thales then Pythagoras, later
Euclid, Archimedes and Apollonius, greatly extended geometry, building a
logical system of theorems and proofs, based on a few axioms. An early result
of this very abstract approach was the Pythagoreans' deduction that the square
root of 2 could not be expressed as a ratio of whole numbers. This was a
result they didn't want to be true, and that no-one would have guessed. Remember,
they believed that God constructed the Universe out of pure numbers! Their
accepting of this new "irrational' truth was a testimony to their honesty and
clear mindedness.
The development of geometry took many generations: it could
only happen because people with some leisure were able to record and preserve
for the next generation complicated arguments and results. They went far
beyond what was of immediate practical value and pursued it as an intellectual
discipline. Plato strongly believed such efforts led to clarity of thought, a
valuable quality in leaders. In fact, above the door of his academy he
apparently wrote: "let no one who cannot think geometrically enter here."
Over this same period, the Greeks began to think scientifically,
meaning that they began to talk of natural origins for phenomena, such as
lightning, thunder and earthquakes, rather than assuming they were messages
from angry gods. Similarly, Hippocrates saw epilepsy as a physical disease,
possibly treatable by diet or life style, rather than demonic possession, as
was widely believed at the time (and much later!).
The geometric and scientific came together in analyzing the
motion of the planets in terms of combinations of circular motions, an approach
suggested by Plato, and culminating in Ptolemy's Almagest. This Greek
approach to astronomy strongly contrasted with that of the Babylonians, who had
made precise solar, lunar and planetary observations for many hundreds of years,
enough data to predict future events, such as eclipses, fairly accurately, yet
they never attempted to construct geometric models to analyze those complex
motions.
Why did Mathematics and Science Grind to a Halt?
Why did the development of science on the ancient world
pretty much end after 800 years, around 200 AD or so? For one thing, the
Romans were now dominant, and although they were excellent engineers, building
thousands of miles of roads, hundreds of military garrisons, and so on, they
did very little science. And, the Greeks themselves lost interest:
Plato's Academy began to concentrate on rhetoric, the art of speechmaking.
Perhaps this had been found to be more valuable for an aspiring leader than the
ability to think geometrically or scientifically, or perhaps better for winning
elections and persuading people. Furthermore, with the conversion of the Roman empire to Christianity around 300 AD, saving souls became a top priority in the
Catholic church. As St. Augustine put it,
"Nor need we be afraid lest the Christian should be
rather ignorant of the force and number of the elements, the motion, order and
eclipses of the heavenly bodies, the form of the heavens, the kinds and natures
of animals, shrubs and stones ... It is enough for the Christian to believe
that the cause of all created things, whether heavenly or earthly, whether
visible or invisible, is none other than the goodness of the Creator, who is
the one true God."
It's a little puzzling to put this together with
Botticelli's picture, showing Augustine looking prayerful but with scientific
instruments in plain sight! (Augustine was very interested in science and
many other unholy things earlier in life.)

St. Augustine, by Botticelli (Wikipedia Commons).
But Some Christians Preserved the Classical Knowledge...
Actually, the story of the treatment of the Greek
mathematical and scientific knowledge by the early Christian church is
complicated, like the church itself. Recall that mathematics and science
effectively ended in Alexandria with the murder of Hypatia in 415 AD, ordered
by the Patriarch Cyril. This same Cyril engaged in a violent theological
quarrel with the Patriarch of Constantinople, Nestorius. The question was the
relative importance of the Virgin Mary. Cyril demanded that she be referred to
as the Mother of God, Nestor would only accept Mother of Christ. This was all
part of a debate about the nature of Christ: did he have two natures, human and
divine, or one nature? Nestor thought two, of which only one, the human, died
on the cross. Getting this right was very important: it was believed that
salvation depended on it. However, the dispute was also (and perhaps
principally) a struggle for power. At the Council of Ephesus in 431, Cyril
arrived early with a large group of strong men, handed out bribes, and got the
assembled bishops to condemn Nestor as a heretic. (Further complications
ensued at later Councils, see for example The Closing of the Western Mind,
Charles Freeman, Knopf, 2002, page 259 on, but it was all bad news for Nestor
and his followers, who became known as Nestorians.)
How the Nestorians Helped Science Survive
What has this got to do with science? It is a crucial link
in the chain. In contrast to most of the rest of the church, the Nestorians
preserved and read the works of Aristotle, Plato, etc., and translated many of
them into Syriac. They felt that clear thinking was useful in theology. Being
declared heretics meant that it was no longer a good idea to stay in the Roman Empire, and, in fact, they were expelled.
Let's briefly review the extent of the Roman Empire to
understand what expulsion implied.
(Note: The maps below were taken from:
//www.roman-empire.net/maps/empire/extent/augustus.html, but this link is now inactive.)
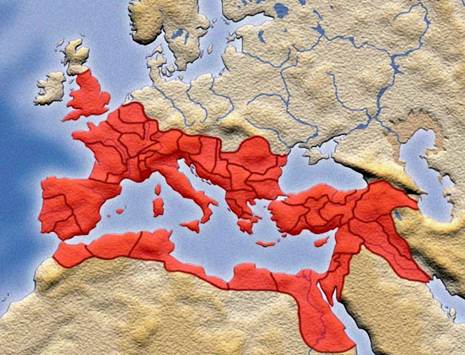
At its greatest extent, in 116 AD, pictured above, notice
that the Empire included almost all of present-day Iraq, essentially to the Persian Gulf. However, this didn't last
long: the Romans' most powerful enemy, the Persians (now known as Iranians),
recaptured the territory after a short Roman occupation.
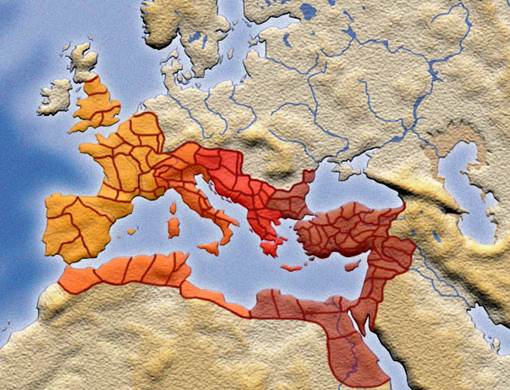
At the time of the death of Constantine, 337 AD, the Empire
was officially Christian. The eastern part of the Empire, ruled from
Constantinople and Greek speaking, became known as Byzantium. The Empire's total
extent is shown below:
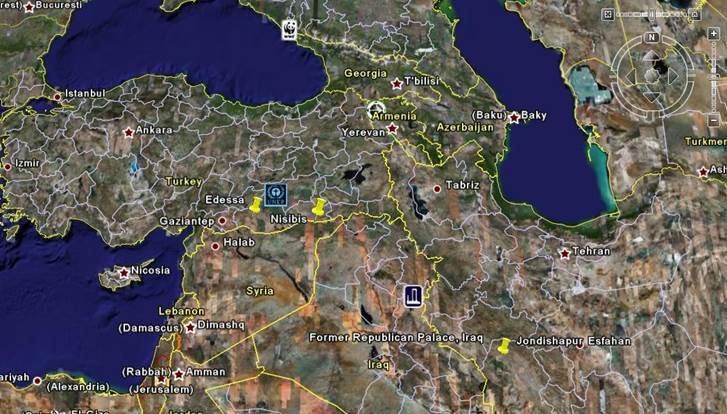
The Nestorians found temporary refuge with Syriac speaking
sympathizers in Edessa (see Google map below, 37 10 N, 38 47 E. Istanbul (top left) is of course Constantinople):
(Nestor was a pupil of Theodore of Mopsuestia in Antioch,
Syria. When Nestor was condemned, these Arab Christians broke with the
Byzantine church, forming the Assyrian Church of the East, see Wikipedia.)
On into Persia
This was all during the time of the second Persian Empire
(226-651), the Sassanid Empire.
The Sassanid Persian kings saw an opportunity to handle
their own considerable number of Christian subjects better. They granted protection
to Nestorians in 462, then in 484, they executed the Bishop of Nisibis (37 04
N, 41 13 E) (who was anti-Nestorian, pro-Byzantine) and replaced him with a
Nestorian. (This is from Wikipedia.)
The Nestorians settled in the Persian Empire, moving eventually to Gundishapur
(near modern Dezful, at 32 25 N, 48 26 E). These Nestorians sent out many missionaries,
for example reaching China in 635, and even Korea, and founding many churches, traces still
remain today. (However, foreign religions were suppressed in China in the 800's.)
The academy at Gundishapir had Syraic as the working
language. Under a Sassanid monarch, Khosrau I, 531-579 AD, it became famous
for learning. Although Khosrau I was a Zoroastrian, the dominant Persian
religion, he was tolerant of all religions, in fact one of his sons became a
Christian. He greatly improved the infrastructure, building palaces, strong
defenses, and irrigation canals. He encourages science and art, collecting
books from all over the known world, and introducing chess from India.
(Trivial Fact: Checkmate is a corruption of the Persian shah mat,
meaning the king is dead.) He had Syriac and Greek works translated into
Persian. He also sent a famous physician Borzuyeh to India
to invite Indian and Chinese scholars to Gundishapur.
The Advent of Islamic Rule
In 622, the prophet Muhammad left hostile Mecca to found his
own theocratic state in Medina (just over two hundred miles to the north, both
in western Saudi Arabia). He readily attracted converts, and built an army
that captured Mecca eight years later. He died in 632, but his armies
continued to conquer. Both Romans and Persians were by this point rather weak
militarily, having spent decades fighting each other. The Sassanid dynasty
fell to Muslim Arab armies in 638 AD. Alexandria was conquered in 642. These
Muslims, although at war with Byzantium, were tolerant of their ethnic
brethren, the Arab Christians. The first dynasty, the Umayyad (660-750),
centered in Damascus, included Hisham ibn Abd as-Malik, who encouraged the
arts, education, and translation of numerous literary and scientific
masterpieces into Arabic (Wikipedia). (The Muslim Empire was now vast: a
Hindu rebellion in Sindh was subdued; at the same time Umayyad armies went
north from Spain, but were defeated at Tours, France, in 732. It has been
argued that if the Arab armies had won at Tours, all Europe would have become
Islamic, and still would be.)
In 749, a second dynasty, the
Abbasid caliphate, began. In 762 the
Abbasid Caliph al-Mansur built a magnificent new capital: Baghdad. Al-Mansur
emulated the Persian rulers, building a palace library like the Sassanid
Imperial Library, except that now everything was to be translated into Arabic.
Harun ar-Rashid, Caliph from 786 to 808, sent agents to buy Greek manuscripts
from Constantinople, to be translated into Arabic. At the same time, the Siddhantas
wrrived from India: a set of Indian astronomical works, including
trigonometric tables that likely originated with Hipparchus, and had then found
their way to the Greek cities in India and Afghanistan founded by Alexander. (It's
worth noting that the first paper mill outside China was built in Baghdad in
794, the secret having been given by prisoners of war from a battle against the
Chinese in Central Asia. In fact, the cheap availability of paper made the
complex Abbasid bureaucracy reasonably efficient.)
Meanwhile, Gundishapur wasn't far away: generously funded
court appointments drew physicians (including al-Mansur's personal physician) and
teachers to Baghdad.
Later, under the Abbasid Caliph al-Ma'mun (813-833), the House
of Wisdom was founded (in 828): a large library and translation center into
Arabic: first from Persian, then Syriac, then Greek. Many works were
translated from Syriac into Arabic, including some Archimedes and all Euclid. Hunayn,
a Christian, from Jundishapur, redid many translations to make them more
readable.
The House of Wisdom: al-Khwarismi
Perhaps the most famous scholar from the House of Wisdom is
Al-Khwarismi (780-850). The word algorithm, meaning some kind of
computational procedure, is just a mangling of his name. This is because he
wrote the book that introduced the Hindu numbering system (now known as Arabic)
to the Western world, and medieval scholars used his name to refer to routines
for multiplication using Arabic numbers, far more efficient than anything
possible with the previously used Roman numerals!
He also wrote the book on algebra: that word is actually
al-jabr meaning completion. (We'll see below why this is an appropriate
term.) Actually, he didn't use symbols to denote unknown quantities, now the
essence of algebra. Ironically, such symbols had been used by the Greek
Diophantus, in Alexandria, in the 200's AD, but that work was apparently
unknown to the Arabs. Instead, al-Khwarismi stated algebraic problems as word
problems, as the Babylonians had over two millennia earlier, but he also gave
geometric representations of his solutions.
Let's look at one of his examples: x2 + 10x = 39.
(OK, I've cheated by using x: he wrote it all out in words, but his thought
process was as outlined below.)
This he thought of in terms of equating areas: a very
natural approach to something beginning with a square! On the left we have a
square of side x and a rectangle of sides x and 10.
His strategy is to add area to this to make it one big
square: he takes the rectangle and divides it into four equal rectangles
each having sides x and 10/4 = 5/2 He then glues these to the x
square:
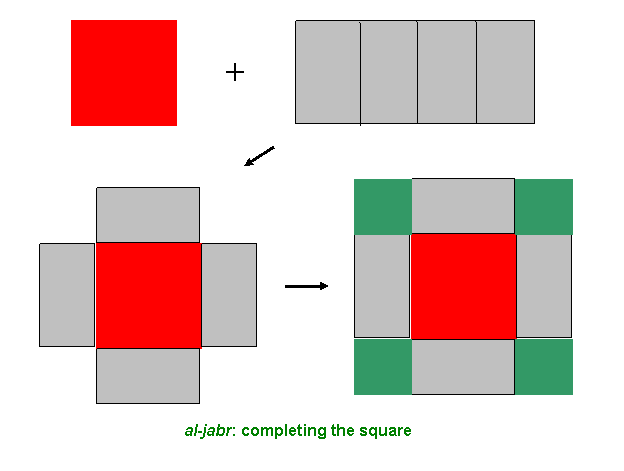
The next step is to extend this to give just one square, by adding
the green bits. But to keep the equation valid, the same amount must of course
be added to the other side. That is, (5/2)x(5/2)x4 is to be added to each side. We
can see that on the left we now have a square of side x + 5. on the right hand
side, we have 39 + 25 = 64 = 8 x 8. Therefore, x + 5 = 8, and x = 3.
So by adding to both sides we have completed the square,
and al-jabr is this adding to get completion. Negative numbers were not
in use at that time, so quadratics like x2 = 10x + 39, for example, were treated
separately, and several distinct cases had to be explained.
It's not clear that al-Khwarismi's own contribution, by
which I mean really new mathematics, was great, but his influence was
tremendous: his presentation of algebra, and of the Arab numerals, sparked much
further mathematical development, both in Baghdad and, later, in the West, as
we shall see.
previous
index
next




