Damped Driven Pendulum V: Poincaré Section
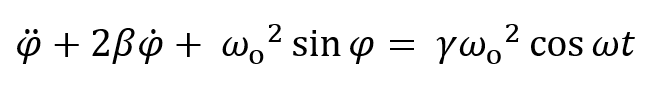
The previous applet showed phase space orbits, which were sometimes quite complex--but what really interests us at the moment is relatively simple: the successive doubling of orbital period and the approach to chaos. For this particular purpose, the orbital details are too much information!
To focus on what's essential, Poincaré plotted a single point from each cycle, this is now called a Poincaré section, just slicing through the orbit.
Following his approach, we plot a series of points in state space: first, P0 = (φ0, ̇φ0) at the initial time t = 0, then P1 = (φ1, ̇φ1) precisely one cycle later, and so on, points one cycle apart, P2 = (φ2, ̇φ2), etc.
As mentioned earlier, knowing the position P = (φ, ̇φ) in state space is not enough information to plot the future orbit, we also need to know the phase of the driving force. But by plotting points one cycle in time apart, they all see the same phase driving force, so the transformation that takes us from P0 to P1 just repeats on going from P1 to P2, etc. (If you've come across the logistics map in chaos theory, you'll notice this has the same mathematical structure: x, f(x), f(f(x)), f(f(f(x)))), etc.)
Remember the whole orbit is really three dimensional, in (φ, ̇φ, ψ) space, ψ being the drive phase. Think of it as in a cylinder: the base is the (φ, ̇φ) plane we've been plotting, ψ measures the height, the sections are slices at different heights. (Actually it's cyclic, so a torus might be a better picture than a cylinder.)
Walk Through
The applet, like the previous one, is preset with γ = 1.081 and so gives a four-cycle, that is, four dots. (There are initial transients, remove them by pressing "Hide Trace" then "Show Trace" after a few seconds running.) The slider just above this text is the phase at which the Poincaré section is taken--move this around slowly to see how the whole orbit, as shown in the previous applet, is made of these sections.
To see the dots better, while the applet is running press Toggle Origin/Scale, move the dots closer to the center of the screen, then scale up. (And, turn off the "Current" button.) Leave the position and scaling where they are, and go to 1.0826 to see an eight-cycle (again, press Hide Trace then Show Trace to get rid of transients.) Then 1.08275 gives a 16-cycle, admittedly barely discernible, then 1.0829 is clearly chaos, not discrete points any more. Now go to 1.1: you will have to set the scale back to 1 to see the whole curve. Then 1.2: this is a strange attractor! Run for say, 20000 cycles, you can see some structure by scaling up and moving around. Going to 1.3, we're back to a single cycle. (Taylor, fig 12.18, gives a map in γ space.)
To reproduce Taylor's fig 12.29 set γ= 1.5, 2β = 0.375, range = 2π, be sure the Scale = 1, and run for a few seconds, while running press "Hide Trace", then "Show Trace" (to get rid of transients). The general shape will appear after 2000 or so cycles, but to get Taylor's level of detail needs much more, say, 60,000, as he used. You can then use origin shift and scaling to see his fig 12.30, but not as well-defined -- this applet cannot generate all the fine detail in his fig. 12.31.
Of course, there's a vast field to explore here. (We reproduced Taylor's attractor partly to confirm the reliability of the applet.) For starters, try varying the damping as well as the driving force. Find what happens to the strange attractor at 2β = 0.75 and above!
Here's the relevant lecture, which includes more details.
Program by: Carter Hedinger