48 High Frequency Limit, Plasma Frequency
Jackson 7.5D. Our presentation here differs somewhat from Jackson’s in that we find it convenient, as in our previous lectures, to work and present results using the wave impedance
Plasma Frequency: Phase Velocity and Impedance
Well above the highest frequency of the molecular oscillators in the Lorentz type model, the permittivity (from the previous lecture) tends to a simple form we’ll call :
This is called the plasma frequency, as explained below, and systems for which this oscillation predominates are called plasmas.
Two important examples of plasmas are the ionosphere, and the electron gas in some conductors.
At these high frequencies, the phase velocity
becomes
and the impedance
Notation! We will denote the electron density by Jackson uses we’ll reserve for impedance in these notes.
Understanding the Plasma Frequency: Longitudinal Oscillations

In this frequency range, the electrons jiggle back and forth so fast the "springs" and damping in the molecular oscillators are irrelevantit's like a gas of free electrons. (We also assume here that collisions between electrons are at a lower frequency.)
Imagine a unit cube of material: suppose all the electrons are displaced by positive If the electron density is and the electron charge there is a "surface" charge density on the positive side, minus that on the other side, consequently an electric field This will give the electrons an acceleration and hence simple harmonic motion, at this plasma frequency.
Notice this is a longitudinal oscillation, more like a sound wave than a light wavebut with an important difference. If we imagine the electrons to be in sheets perpendicular to the direction of the wave, then the interaction between sheets doesn’t drop off with distance (recall electric field from a plane of charge). This is in contrast to the mechanical forces as a sound wave passes through a solid or a liquid. It follows that the longitudinal plasma wave frequency depends only weakly on the wavelength of a disturbance (what dependence there is comes from compressibility, which has a quantum mechanical origin).
Note also that the field has the form which has no curl, so there is no accompanying magnetic field. For obvious reasons, these waves are sometimes called “electrostatic waves”. (However, in some systems they can generate radio waves via nonlinear mechanismswe won’t pursue this further here.)
The electron density in the ionosphere is 10181022/m3 so is in the range 60 GHz to 6 THz (quoting Jackson here). For metals, the density is of order 1029/m3, the plasma frequency in the ultraviolet (order 1016.)
Transverse EM Waves in a Plasma:
What happens when a light (or other EM) wave enters a plasma?
In this lecture, we’re taking the permittivity to be
We also assume the plasma has no significant magnetic properties, that is, we take
This is a pretty good model for the electron gas in many conducting metals for the appropriate frequency range (including optical and higher), and an excellent model over a wide frequency range for the ionosphere.
As discussed earlier, the two important parameters in analyzing an electromagnetic wave entering or traversing a medium are the wave phase velocity (as in ) and the impedance:
Starting with the kinetic properties, squaring , we find
and so
In contrast to the longitudinal plasma waves, these transverse waves have a frequency depending on wavelength.
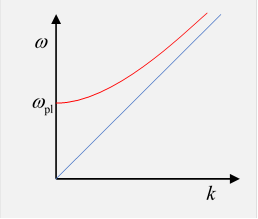
For frequencies far above the plasma frequency, the waves tend to ordinary light (or ultraviolet, etc.) with little contribution from the plasma. However, for frequencies approaching (from above) the group velocity tends to zero, and from and the magnetic field disappears, so we are moving towards an oscillation more like the longitudinal one described above, but now in the transverse direction.
Turning now to the dynamic properties: suppose an ordinary electromagnetic wave, such as light, is traveling through empty space and encounters a plasma. Will some be reflected? In fact, we already have the necessary tools to find out: we know the plasma impedance (assuming we’re in the right frequency range, and taking )
and, assuming normal incidence, we just substitute this in the equations we found in an earlier lecture,
to give the transmitted electric field
Exercise: Using find the transmitted energy using Poynting’s theorem. Find what happens for Then take In particular, look at the fields in this limit.
Transverse EM Waves in a Plasma:
Recall
From
for is negative,
and the wave decays exponentially after entering the plasma,
The wave energy is not being absorbed into the plasma, in our model there is no mechanism to do that, so it has to be fully reflected, easy to confirm using the wave impedance
So is pure imaginary, and the reflected amplitude
has unit modulus, meaning all the energy is reflected, with phase shift
In the limit of zero frequency, the field decays exponentially as stated above, and the field energy has penetration length
Notice, though, that on increasing the frequency of the incoming EM wave, increases, and near the plasma frequency, typically in the ultraviolet, some alkali metals become transparent, at least in thin films, according to R. W. Wood in a 1933 paper, and Born and Wolf, and Jackson calls it drastic (page 314). But gold foil is transparent if thin enough, I can’t find evidence of a thick piece of transparent alkali metal (say, 1 mm), so this search is left as an exercise for the reader.