previous  index  next 

29.  Molecular Polarizability and Electric Susceptibility

    Michael Fowler, UVa

Simple Classical Model for Polarization of a Molecule

We’ve talked about the distortion of charge distribution in a molecule when an electric field is applied, and a real analysis can only be done quantum mechanically, but we can get some idea of the size of the effect from simple classical considerations.  Suppose the solid only contains one kind of polarizable molecule.  Model the molecule as a harmonically bound single electron, spring constant $k,$ so the equation of motion (taking for now just one relevant dimension) is

$m\ddot{x}=-kx=-m{\omega }_0^{2}x.$ 

Imposing an external field, constant force $eE,$ the electron's equilibrium position is shifted by $d,$ where $eE=kd=m{\omega }_0^{2}d.$ 

This generates a dipole moment

${\overrightarrow{p}}_{\text{mol}}=e\overrightarrow{d}=e^2\overrightarrow{E}/m{\omega }_0^2.$

Recall now we defined the electric susceptibility ${\chi }_e$ by

$\overrightarrow{P}={\epsilon }_0{\chi }_e\overrightarrow{E}.$ 

 We define similarly the molecular polarizability ${\gamma }_{\text{pol}}$ by

${\overrightarrow{p}}_{\text{mol}}={\epsilon }_0{\gamma }_{\text{mol}}\overrightarrow{E}.$ 

Now, the polarization density

$\overrightarrow{P}=N{\overrightarrow{p}}_{\text{mol}},$ 

where $N$ is the molecular number density, and this is what we want to find, for a dielectric in an applied  field $\overrightarrow{E}.$ 

But What is the Field at the Molecule?

Our simple model trivially gives the molecular polarization if the molecule is placed in a field of given strength.  But real life is more complicated: focusing on a single molecule, it's surrounded by the other molecules in the solid, they too respond to the imposed external field, so what is the actual field experienced by a single molecule, for given imposed field?

An obvious approach is to think of the atom as being in a small cavity in the dielectric.  So, what is the field in a small cavity in a polarized dielectric?  Thinking more macroscopically, the electric field in the cavity will be the electric field just outside it (but in the dielectric), plus some contribution from the surface charges (resulting from polarization) on the cavity walls. These will have the opposite sign from those on the surface of a piece of dielectric polarized by being in an external field, of course, so will be $\overrightarrow{P}\cdot \widehat{\overrightarrow{n}}$ with $\widehat{\overrightarrow{n}}$ the unit normal to the cavity surface, pointing into the cavity.

Different Shaped Cavities: Cylinder, Pancake, Sphere

 

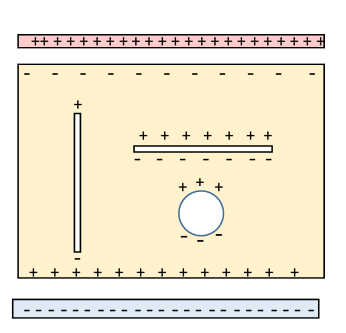
The diagram represents a slab of dielectric between two parallel charged plates, and with three cavities inside. The imposed electric field from the charged plates induces polarization.

With the geometry shown, the actual electric field $\overrightarrow{E}$  within the dielectric is reduced from $V/d$ (the voltage between the plates divided by the separation distance) by a factor $\epsilon ,$ as a result of the layers of bound charge induced immediately next to the charged plates. 

To find the field actually at the molecule, we first imagine it in a small cavity in the dielectric  (we'll consider contributions from immediately adjacent molecules later).  Now the field in a cavity depends on the shape of the cavity: this becomes evident on considering the bound charge excess or deficit at the cavity walls, see the diagram.

A long thin cavity parallel to the polarization will have only small areas perpendicular to the polarization, and these are the only surfaces with unbalanced bound charge, so will make little contribution to the field in the cavity which will therefore be just the electric field $\overrightarrow{E}$ in the dielectric. 

In contrast, the pancake cavity shown will have an increased field $\overrightarrow{E}+\overrightarrow{P}/{\epsilon }_0.$ 

The important spherical cavity is intermediate.

The most natural approach (unless the dielectric is very anisotropic) is to assume a spherical cavity. 

Following Feynman (a lecture you should definitely read) the field in a spherical cavity is easily found by imagining a uniform polarized dielectric as having a spherical cavity plus a plug of the identical material exactly fitting into the cavity. The plug is therefore a uniformly polarized dielectric sphere, so its surface excess bound charge must be generating an internal field ${\overrightarrow{E}}_{\text{plug}}=-\overrightarrow{P}/3{\epsilon }_0,$ from our earlier discussion. 

But really that surface isn’t there, we’re just imagining this plug, so the hole must have exactly the opposite surface charge,  meaning a spherical hole in a uniformly polarized dielectric medium has an internal field from its polarization surface charge of ${\overrightarrow{E}}_{\text{sph hole}}=+\overrightarrow{P}/3{\epsilon }_0.$ Therefore, the total field inside the spherical hole is

$\overrightarrow{E}+\overrightarrow{P}/3{\epsilon }_0.$ 

The Clausius-Mossotti Equation

We’ll now make the assumption that a single polarizable molecule in the dielectric can be thought of as in its own spherical cavity. Therefore, its molecular polarization is given by its susceptibility to the field in such a cavity. This leads to a self-consistent equation for the polarization:

$\overrightarrow{P}=N{\gamma }_{\text{mol}}{\epsilon }_0\left(\overrightarrow{E}+\frac{\overrightarrow{P}}{3{\epsilon }_0}\right),$  and from this:

$\overrightarrow{P}=\frac{N{\gamma }_{\text{mol}}}{1-\frac{1}{3}N{\gamma }_{\text{mol}}}{\epsilon }_0\overrightarrow{E}={\epsilon }_0\chi \overrightarrow{E}=\left(\epsilon -{\epsilon }_0\right)\overrightarrow{E},$  to put in our accumulation of notations. We can now deduce the molecular susceptibility in terms of the dielectric constant:

$\begin{array}{c}\frac{N{\gamma }_{\text{mol}}}{1-\frac{1}{3}N{\gamma }_{\text{mol}}}{\epsilon }_0=\left(\epsilon -{\epsilon }_0\right),\\ N{\gamma }_{\text{mol}}{\epsilon }_0=\left(\epsilon -{\epsilon }_0\right)\left(1-\frac{1}{3}N{\gamma }_{\text{mol}}\right),\\ {\gamma }_{\text{mol}}=\frac{3}{N}\left(\frac{\epsilon -{\epsilon }_0}{\epsilon +2{\epsilon }_0}\right).\end{array}$

This is called the Clausius-Mossotti equation. 

Feynman writes the equation in reverse, that is,

$\kappa -1=\frac{N{\gamma }_{\text{mol}}}{1-\frac{1}{3}N{\gamma }_{\text{mol}}},$  where

$\kappa =1+\chi =\epsilon /{\epsilon }_0$  is the dielectric constant.

But What About the Molecule's Nearest Neighbors?

Is it really OK to replace all the other molecules by just a smooth dielectric with a spherical hole? 

Maybe the immediate neighbor molecules need to be treated more carefully?

Jackson introduces a term for this near field, that is, how much it deviates from the continuum approximation.  However, for a simple cubic lattice, Lorentz proved that the near field is zero$—$the symmetry gives complete cancellation.  (Visualize one point in a simple cubic lattice, with dipoles, all pointing the same way, at the six neighbor points. Add together the six electric field contributions at the origin.) To get any further for other lattices requires serious quantum mechanical input, and in fact the contribution is often small, so we'll stop here.

Polarizability of Molecules Having Permanent Dipole Moments

Many molecules have permanent electric dipole moment, in particular water: the hydrogen atoms attach to the oxygen like Mickey Mouse ears, and the hydrogen electron orbits are pulled somewhat towards the oxygen nucleus, leaving the hydrogen protons' charge not locally fully compensated.  

 

However, for water at room temperature, even a strong electric field will only cause small alignment of the dipole moments, because the energy of alignment is far smaller than $k_{B}T$.  

The statistical probability of any particular direction of dipole orientation in a field $\overrightarrow{E}$ along the $z$ axis is proportional to $e^{-H/k_{B}T}=e^{p_{0}E\cos \theta /k_{B}T},$ from which (putting the appropriate normalization factor into the denominator so that the total probability adds up to one)

$〈p_{\text{mol}}〉=\frac{{\displaystyle \int d\Omega \left(p_{0}cos\theta \right)e^{p_{0}E\cos \theta /k_{B}T}}}{{\displaystyle \int d\Omega e^{p_{0}E\cos \theta /k_{B}T}}}$  and for ordinary temperatures where $k_{B}T\gg p_{0}E$ we can just take the first term in the exponential series, and using $〈{\cos }^2\theta 〉=\frac{1}{3}$ over a spherical surface ( $〈z^2〉=\frac{1}{3}$ on the unit  sphere), we get

$〈p_{\text{mol}}〉=\frac{p_0}{3}\frac{p_{0}E}{k_{B}T}=\frac{p_0^2}{3k_{B}T}E.$  For polar molecules, then, the polarizability is linear in inverse temperature.  

Of course, the analysis above neglects the interaction between water molecules: that's a lot more difficult to include.  Density functional calculations suggest a correction of order 10% in the liquid.

Electrostatic Energy in Dielectric Media

We know that for charges in free space, the total energy is

$W=\frac{1}{2}{\displaystyle \int \rho \left(\overrightarrow{r}\right)\phi \left(\overrightarrow{r}\right)d^{3}r.}$ 

Recall that the half comes about because we gradually build up the charges from zero, and the potential depends linearly on the charge. 

It’s a little more complicated if there is a dielectric medium present, since there will be energy of polarization in the medium itself, not just the electrostatic energy of the free charge distribution.  

Trying the same “bring the charge up gradually” approach with a dielectric present, suppose at some stage we have density $\rho \left(\overrightarrow{r}\right)$ of free charge, and the actual potential is $\phi \left(\overrightarrow{r}\right),$ resulting from this free charge plus whatever polarization contribution it causes. Now suppose we bring up an extra charge increment $\delta \rho \left(\overrightarrow{r}\right).$ To leading order, that takes work

$\delta W={\displaystyle \int \delta \rho \left(\overrightarrow{r}\right)\phi \left(\overrightarrow{r}\right)d^{3}r.}$ 

Since $\overrightarrow{\nabla }\cdot \overrightarrow{D}=\rho ,\delta \rho =\overrightarrow{\nabla }\cdot \delta \overrightarrow{D}$ and

$\delta W={\displaystyle \int \overrightarrow{\nabla }\cdot \delta \overrightarrow{D}\phi \left(\overrightarrow{r}\right)d^{3}r=-}{\displaystyle \int \delta \overrightarrow{D}\cdot \overrightarrow{\nabla }\phi \left(\overrightarrow{r}\right)d^{3}r}={\displaystyle \int \delta \overrightarrow{D}\cdot \overrightarrow{E}{d}^{3}r}.$ 

If the medium is linear, $\delta \overrightarrow{D}\cdot \overrightarrow{E}=\frac{1}{2}\delta \left(\overrightarrow{D}\cdot \overrightarrow{E}\right)$ and

$W=\frac{1}{2}{\displaystyle \int \overrightarrow{D}\cdot \overrightarrow{E}{d}^{3}r}$ 

(Check: correct in vacuum, $\overrightarrow{D}={\epsilon }_0\overrightarrow{E}.$ )   Physically, it takes work to build up the electric field, and when a dielectric is present it takes more work to polarize that, pulling apart the positive and negative charges.

Jackson next addresses the problem of energy change of a chunk of dielectric, containing no free charge, placed in an electric field ${\overrightarrow{E}}_0$ generated by fixed charges. The dielectric has no net dipole moment density in zero field, but gradually building up the field and assuming the induced polarization (dipole moment density) is linear in the field gives the by-now-familiar factor of one-half:

$W=-\frac{1}{2}{\displaystyle \int \overrightarrow{P}\cdot {\overrightarrow{E}}_0{d}^{3}r.}$ 

How does this differ from the previous case? We now have an existing electric field from fixed external charges that stay constant. Let's say we take a small piece of dielectric, and move it gradually from outside the field to somewhere where there is field $\overrightarrow{E}.$ As it moves, assume the polarization adiabatically follows the field, incrementally the energy decreases, changing by $-{\overrightarrow{E}}_0\cdot \Delta \overrightarrow{P}.$  (Just as a compass needle goes to the lowest energy state.)  As it moves from no field to $\overrightarrow{E},$ positive energy is being stored in its polarization, $\frac{1}{2}\overrightarrow{P}\cdot {\overrightarrow{E}}_0,$ as before, but it orients its moment in the field to lower its energy by $\overrightarrow{P}\cdot {\overrightarrow{E}}_0.$ Wait: what happened to that energy? Assuming it's moving to a stronger field, it's pulling you along, it's doing work. So dielectric dust in a varying field will move in the direction of strengthening field.

We can use the fixed external field ${\overrightarrow{E}}_0$ rather than the actual field $\overrightarrow{E},$ the difference is just mutual interactions between dipole elements in the dielectric, they will cancel in finding the energy.

Zangwill spells this out (p 183): he puts a piece of dielectric into a field ${\overrightarrow{E}}_0$ and writes the total energy change as a sum of three terms, $\Delta U_E=U_{\text{ext}}+U_{\text{int}}+U_{\text{self}},$ The first term is just the potential energy of the dipoles in the preexisting field (regardless of history) $U_{\text{ext}}=-{\displaystyle \int d^{3}r\overrightarrow{P}\left(\overrightarrow{r}\right)\cdot {\overrightarrow{E}}_0\left(\overrightarrow{r}\right).}$ The term $U_{\text{self}}$ is the total mutual energy of the collection of dipoles making up the piece of dielectric, so the electric field ${\overrightarrow{E}}_{\text{ind}}\left(\overrightarrow{r}\right)$ is that field generated by the dielectric in response to the external field ${\overrightarrow{E}}_0,$ and $U_{\text{self}}=-\frac{1}{2}{\displaystyle \int d^{3}r\overrightarrow{P}\left(\overrightarrow{r}\right)\cdot E_{\text{ind}}\left(\overrightarrow{r}\right).}$  The interaction term is then given by

$U_{\text{int}}={\displaystyle \int d^{3}r{\displaystyle \underset{0}{\overset{P}{\int }}\overrightarrow{E}\cdot \delta \overrightarrow{P}}}=\frac{1}{2}{\displaystyle \int d^{3}r\overrightarrow{P}\left(\overrightarrow{r}\right)\cdot \left[{\overrightarrow{E}}_0\left(\overrightarrow{r}\right)+{\overrightarrow{E}}_{\text{ind}}\left(\overrightarrow{r}\right)\right]}.$

We see explicitly that the ${\overrightarrow{E}}_{\text{ind}}$ terms do indeed cancel.

Exercise:

   

A slab of dielectric ( $\epsilon$ )  is gradually moved into the space between parallel capacitor plates, area $A,$ separation $d.$ Find the energy change (i) if the plates carry fixed charge, and initial potential difference $V_0$  (ii) if the plates are maintained at potential difference $V_0$ by an attached battery.