70. Cherenkov Radiation, Bremsstrahlung, Etc.

Introduction

Jackson chapters 13 and 15 are mainly concerned with radiation arising from the passage of a charged particle through matter: obviously, a subject of huge technological importance, from X-rays to reactor shielding. However, in contrast to most of the course, this is an area where exact solutions are unavailable: the relative importance of various scattering effects, and some complicating many body factors need to be weighed. Furthermore, quantum effects can be important. Consequently, a full treatment of any one of these phenomena, for example how far a charged particle will penetrate on going into matter, takes much calculation. Unfortunately we do not have time to do this, so we'll settle for a short account of Cherenkov radiation, and some remarks about other radiation phenomena.

Cherenkov Radiation

Shock Wave

When a charged particle moves through a transparent medium at a speed greater than the phase velocity of light in the medium, radiation is emitted. This is called Cherenkov radiation, after Pavel Cherenkov, who was the first to detect it experimentally in 1934. He received the Nobel Prize for this discovery, shared with the two theorists, Tamm and Frank, who explained the effect. (In fact, it had been predicted by Heaviside in 1888.)

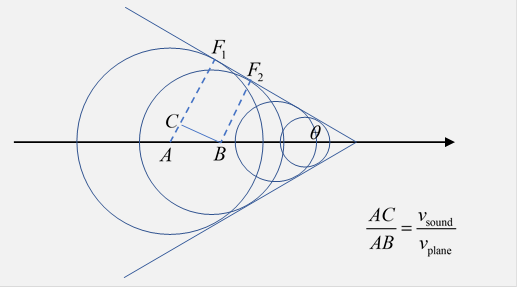
A simple picture of Cherenkov radiation is provided by comparing it with the shock wave generated by a supersonic airplane. (Check out this animation.) The sound waves emitted at each instant radiate outwards in a spherical wave in the air, the plane outstrips the outgoing wave and continues to generate spheres, the envelope of these spheres is the supersonic shock wave, a cone, with semi angle given by $\sin θ = \frac{v_{sound}}{v_{plane}} .$

It's called the Mach cone. Here is a picture of where the leading edge of the radiation is at some instant of time.

The shock front itself is made of waves emitted at different times, but of course reaching the sloping line (say at F₁ and F₂) simultaneously $—$ because as the plane flew from A to B, the wave emitted at A progressed to C.

Going now to the analogous problem of a charged particle moving through a dielectric material faster than the speed of light in that material, it turns out the overall Cherenkov radiation loss is small (but important!), so the particle has only slight deceleration, we can take its speed constant in this analysis. The moving charge causes a dielectric shielding response, obviously time-dependent, and this is the excitation that travels outwards from the immediate vicinity of the particle.

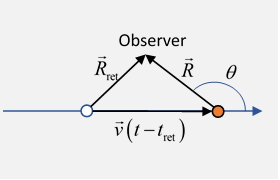
We can analyze this in the usual way, the potential and field observed at current time $t$ at displacement $\vec{R}$ from the current particle position comes from the particle + shielding at $t_{ret},$ the observer being at ${\vec{R}}_{ret}$ relative to the particle position at that time (see drawing) so

$t - t_{ret} = \frac{R_{ret}}{c / n} .$ However, this is different from our earlier analysis of fields from a moving charge. Glancing at the first figure above, we can see that at any point within the cone two of the circles intersect, an observer there will see two signals at the same instant from the moving charge at different earlier times! Or, in line with our previous analysis of the world line of a particle always being inside the light cone, the "light cones" in the dielectric are narrower, and a particle moving faster than the speed of light in the medium can intersect the cone twice (at a steady velocity).

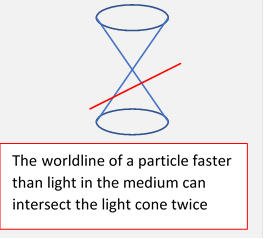
The two points of intersection coincide for an observation point on the cone, so there is a heavy concentration of energy there.

To find the electric and magnetic fields, the Lienard-Weichert potentials still work if we replace $ε_{0} \to ε, μ_{0} \to μ, {\vec{β}}_{n} = \vec{v} / c_{n} = \vec{v} / (c / n) .$ We'll assume for now that $ε, μ$ are frequency-independent, so we can write

$φ (\vec{r}, t) = \frac{1}{4 π ε_{0}} {[\frac{q}{R - {\vec{β}}_{n} \cdot \vec{R}}]}_{ret}, \vec{A} (\vec{r}, t) = \frac{μ}{4 π} {[\frac{q \vec{v}}{R - {\vec{β}}_{n} \cdot \vec{R}}]}_{ret} .$ Notice we have to put the observer inside the Mach cone, or nothing will be observed.

From the diagram, and squaring $R_{ret} = |\vec{R} + \vec{v} (t - t_{ret})|,$ we find a quadratic equation for $t - t_{ret},$ with roots

$t - t_{ret} = \frac{- \vec{v} \cdot \vec{R} \pm \sqrt{{(\vec{v} \cdot \vec{R})}^{2} - (v^{2} - c_{n}^{2}) R^{2}}}{v^{2} - c_{n}^{2}} \geq 0.$ Now for Cherenkov radiation, we also need $\vec{v} \cdot \vec{R} < 0, \sin θ \leq \sin θ_{C} = 1 / β_{n} .$ (This last being when the two roots coincide).

We are not going to go through the detailed derivation of the electric field from the contribution of the two retarded points here. Jackson’s treatment is not very clear, I recommend that in Zangwill: he finds $φ, \vec{A}$ by feeding in these two values, and so can find the fields. The electric field is indeed singular on the shockwave front, but its nonzero value inside the cone points the wrong way $—$ towards rather than away from the charge. There is a simple explanation for this: as the charge passes, it polarizes the medium, but it's moving so fast that immediately behind it is a net negative charge density that takes time to relax, in fact it is part of the outwardly propagating wave.

Landau (Continuous Media) has a different approach: he is interested in estimating the intensity of the Cherenkov radiation. He finds the electric field by the standard method, adjusted to include the permittivity, then finds the energy loss rate from the force of this field on the particle.

The sharp nature of the shock wave front (which is actually somewhat fuzzed out by frequency variations in dielectric response, ignored here) suggests that the radiation covers a wide range of frequencies, and over the visible range it tends if anything to increase with frequency, so the light appears blue.

Uses of Cherenkov Radiation

It is widely used in biochemistry and medicine, radioactive markers emit energetic particles which are traveling faster than light in biomaterials (essentially, water). Cherenkov radiation is used to detect them.

It is central to neutrino searches: for example, IceCube, at the south pole. One cubic kilometer of ice, with many Cherenkov radiation detectors. Finds a few dozen neutrinos a year.

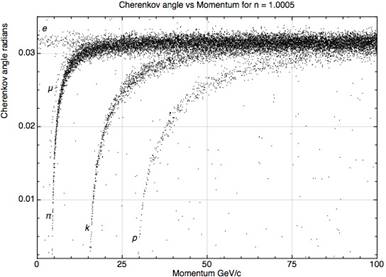
It’s used in many high energy experiments to find velocity of particles of known momentum, hence find their mass, in identifying decay fragments from collisions. The dielectric medium is typically a gas, with $ε = 1.0005 ε_{0},$ say, so there won't be any Cherenkov radiation if the particle is traveling slower than $c / 1.0005,$ $γ < 30$ or so.

Bremsstrahlung

Just a few remarks...

We've analyzed the radiation emitted by an accelerating particle, and how that limits accelerator design. A closely related topic, of arguably equal importance, is the radiation emitted by a decelerating particle. The formulas are the same ones we have found, remember what appears is the square of the acceleration, the sign doesn’t matter. The radiation is called bremsstrahlung, the German for braking radiation, since it is emitted as the charged particle decelerated on interacting with other particles. The Wikipedia article is worth looking over.

The first use of bremsstrahlung was X-rays, accidently discovered in the 1890's when a high voltage (some kilovolts) discharge tube (Crookes tube) was found to spoil boxed photograph film kept nearby (accounts of the discovery differ…for more details, see my notes here). The rays came from energetic electrons hitting the metal anode and rapidly decelerating on being deflected by close encounters with the electric fields of the nuclei. (Imagine the electron as one end of a rapidly changing dipole, anchored at the nucleus.) The relativistic correction is rather small at these energies, so the Larmor formula is reasonably good.

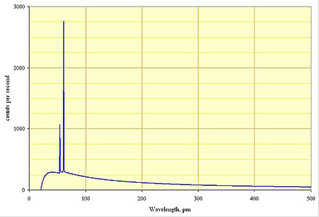
(Typical X-ray spectra also include some sharp lines, from inner shell electrons being ejected, then replaced with other electrons making the transition down. There is a sharp high energy cutoff in the observed radiation, a purely quantum effect $—$ a photon cannot have more energy than an incoming electron, not part of this course.)

Plasma cooling, including opacity

A hot plasma cools down mainly by bremsstrahlung emission from the electrons colliding with ions. In clusters of galaxies, maybe 15% of the total mass is in hot gas away from stars. Bremsstrahlung (mostly X-ray) is observed from the region around and between the galaxies. These regions are transparent to galaxies further away, so must be mostly plasma, as opposed to hot dust clouds.

In a tokomak-type plasma, bremsstrahlung would cause rapid cooling, but that dense plasma is far from transparent, so much of this energy is reabsorbed.

Various Other Generators of Radiation

Particles accelerated in a synchrotron can be caused to radiate by going linearly through a wiggler. This is a sequence of alternating magnets causing the path to deviate from a straight line to a sinusoidal path. (In practice, this is a straight section in the storage "ring", clearly not a circular ring.) The consequent back and forth oscillation generates dipole radiation, the frequency determined by particle speed and magnet spacing.

The free electron laser (FEL) is essentially a wiggler with reflecting mirrors at the two ends, so the radiation intensity builds coherently to a strength where there is ponderomotive feedback on the particle current.

Transition radiation (TR) is generated when a fast particle goes into a material with a different refractive index. The electric field lines will be changed, and connecting the old lines to the new ones will generate radiation, analogous to Purcell's analysis of radiation from a nonrelativistic accelerating charge.

The Smith-Purcell Effect (named after a graduate student!) is the generation of radiation by a fast charged particle moving just above a metal diffraction grating. The sequential response of the strips of metal will generate outgoing coherent radiation at certain angles. The is currently used for terahertz radiation, a frequency range difficult to generate otherwise.

previous index next