3. Fermat’s Principle of Least Time
Michael Fowler
Another Minimization Problem…
Here's another minimization problem from the 1600's, even earlier than the brachistochrone. Fermat famously stated in the 1630’s that a ray of light going from point A to point B always takes the route of least time—OK, it's trivially true in a single medium, light rays go in a straight line, but it's a lot less obvious if, say, A is in air and B in glass. Notice that this is closely related to our previous topic, the calculus of variations—if this is a minimal time path, varying the path by a small amount will not change the time taken to first order. (Historical note: actually what amounted to Fermat’s principle was first stated by Alhazen, in Baghdad, around 1000 AD.)
This seemed very mysterious when first extensively discussed, in the 1600's. In the last part of that century, and through the 1700's, Newton was the dominant figure, and he believed that light was a stream of particles. But how could the particle figure out the shortest time path from A to B?
In fact, there was one prominent physicist, Huygens', who thought light might be a wave, and, much later, this turned out to be the crucial insight. The main objection was that waves go around corners, at least to some extent, it seemed that light didn't. (Also, they exhibit diffraction effects, which no one thought they'd seen for light, although in fact Newton himself had observed diffraction—Newton's rings—but had an ingenious explanation, as always, of why his particle picture could explain what he saw.) Anyway, in 1678, Huygens' suggested the following picture: it's a simple beginning to understanding wave propagation, most notably it omits phases (later added by Fresnel) but it was a beginning.
Huygens' Picture of Wave Propagation
If a point source of light is switched on, the wavefront is an expanding sphere centered at the source. Huygens suggested that this could be understood if at any instant in time each point on the wavefront was regarded as a source of secondary wavelets, and the new wavefront a moment later was to be regarded as built up from the sum of these wavelets. For a light shining continuously, the process just keeps repeating.
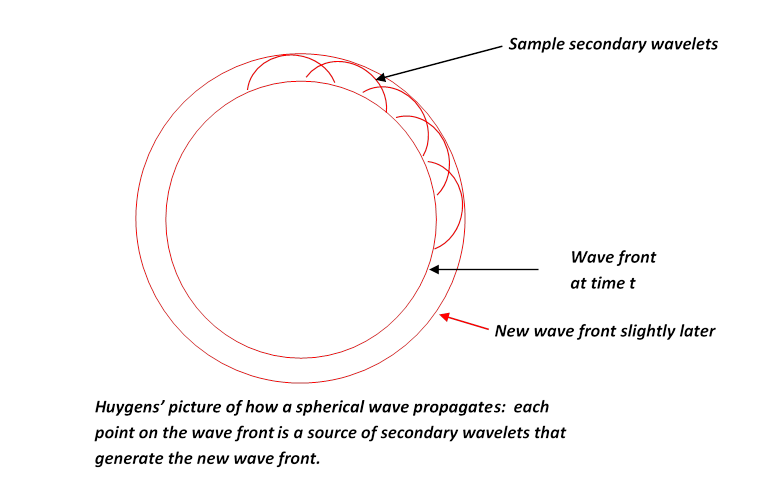
You might think that if a point on the wavefront is a new source, wouldn't the disturbance it generates be as likely to go backwards as forwards? Huygens did not address this point. In fact, it's not easy to give a short satisfactory answer. We'll discuss propagation of light (and of course other electromagnetic waves) fully in the second semester of E&M.
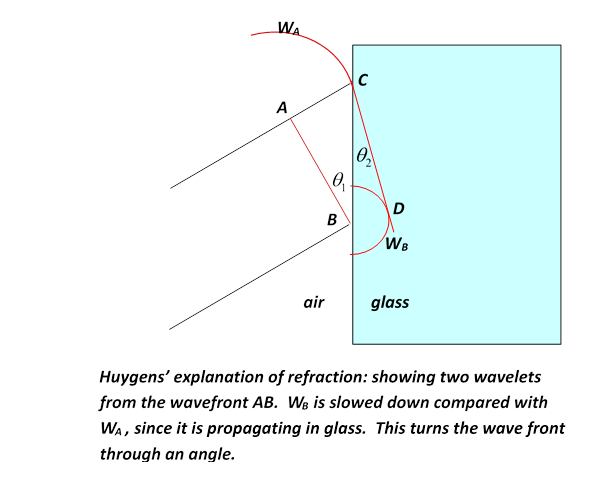
Huygens' principle does explain why the wavefront stays spherical, and more important, it explains refraction—the change in direction of a wavefront on entering a different medium, such as a ray of light going from air into glass. Here's how: If the light moves more slowly in the glass, velocity instead of , with , then Huygens' picture predicts Snell’s Law, that the ratio of the sines of the angles to the normal of incident and transmitted beams is constant, and in fact is the ratio . This is evident from the diagram below: in the time the wavelet centered at A has propagated to C, that from B has reached D, the ratio of lengths AC/BD being . But the angles in Snell’s Law are in fact the angles ABC, BCD, and those right-angled triangles have a common hypotenuse BC, from which the Law follows.
Notice, though, the crucial fact: we get Snell's law on the assumption that the speed of light is slower in glass than in air. If light was a stream of particles, the picture would have to be that they encountered a potential change on going into the glass, like a ball rolling on a horizontal floor encountering a step, smoothed out a bit, to a different level. This would give a force perpendicular to the interface on going from one level to the other, and if the path is bent towards the normal, as is observed, the ball must speed up—so this predicts light moves faster in glass. It wasn't until the nineteenth century, though, that measuring the speed of light in glass (actually I think water) was technologically possible.
In fact, even in the early nineteenth century, the wave nature of light was widely doubted. Fresnel greatly improved Huygens' crude picture, fully taking into account the interference between secondary wavelets having different phases. One of the principal skeptics of the wave theory, the mathematician Poisson, pointed out that it was obvious nonsense because, using Fresnel's own arguments, it predicted that in the very center of the dark shadow of a sphere illuminated by a point source of light, there should be a bright spot: all the "light waves" grazing the edge of the sphere would generate secondary wavelets which would land at that spot in phase. A bright spot at the center of the dark disk seemed obvious nonsense, but an experimentalist colleague in Paris, Arago, decided to try the experiment anyway—and the spot was there. It's now called the Poisson spot, and it gave a big boost to the wave theory in France (it was already fully accepted in England, where Thomas Young did the double slit interference pattern, and compared it to the wave pattern in a similarly configured ripple tank, presenting the results to the Royal Society in 1803).
Fermat’s Principle
We will now temporarily forget about the wave nature of light, and consider a narrow ray or beam of light shining from point A to point B, where we suppose A to be in air, B in glass. Fermat showed that the path of such a beam is given by the Principle of Least Time: a ray of light going from A to B by any other path would take longer. How can we see that? It’s obvious that any deviation from a straight line path in air or in the glass is going to add to the time taken, but what about moving slightly the point at which the beam enters the glass?
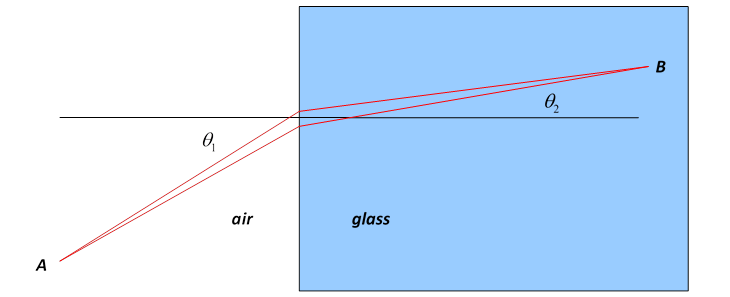
Where the air meets the glass, the two rays, separated by a small distance CD = d along that interface, will look parallel:
(Feynman gives a nice illustration: a lifeguard on a beach spots a swimmer in trouble some distance away, in a diagonal direction. He can run three times faster than he can swim. What is the quickest path to the swimmer?)
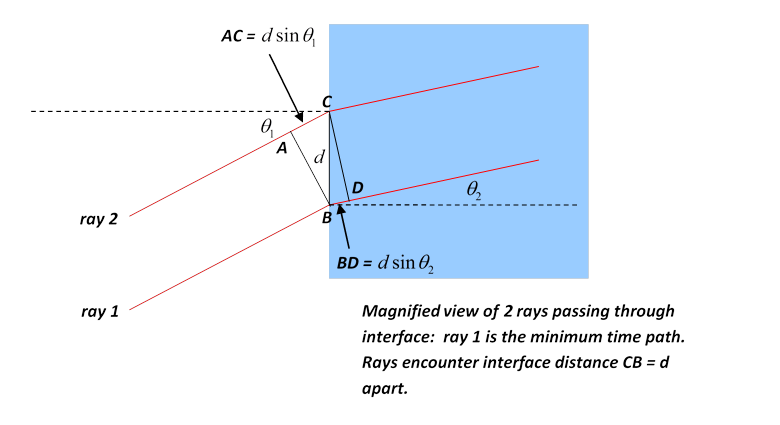
Moving the point of entry up a small distance , the light has to travel an extra in air, but a distance less by in the glass, giving an extra travel time . For the classical path, Snell’s Law gives , so to first order. But if we look at a series of possible paths, each a small distance away from the next at the point of crossing from air into glass, becomes of order away from the classical path.
But now let's take a closer look at the Huygens picture of light propagation: it would suggest that the light reaching a point actually comes from many wavelets generated at different points on the previous wavefront. A handwaving generalization might be that the light reaching a point from another point actually includes multiple paths. To keep things manageable, let's suppose the light from A to B actually goes along all the paths that are straight in each medium, but different crossing point. Also, we'll make the approximation that they all reach B with equal amplitude. What will be the total contribution of all the paths at B? Since the times along the paths are different, the signals along the different paths will arrive at B with different phases, and to get the total wave amplitude we must add a series of unit 2D vectors, one from each path. (Representing the amplitude and phase of the wave by a complex number for convenience—for a real wave, we can take the real part at the end.)
When we map out these unit 2D vectors, we find that in the neighborhood of the classical path, the phase varies little, but as we go away from it the phase spirals more and more rapidly, so those paths interfere amongst themselves destructively. To formulate this a little more precisely, let us assume that some close by path has a phase difference from the least time path, and goes from air to glass a distance away from the least time path: then for these close by paths, , where depends on the geometric arrangement and the wavelength. From this, the sum over the close by paths is an integral of the form . (We are assuming the wavelength of light is far less than the size of the equipment.) This is a standard integral, its value is , all its weight is concentrated in a central area of width , exactly as for the real function .
This is the explanation of Fermat’s Principle—only near the path of least time do paths stay approximately in phase with each other and add constructively. So this classical path rule has an underlying wave-phase explanation. In fact, the central role of phase in this analysis is sometimes emphasized by saying the light beam follows the path of stationary phase.
Of course, we’re not summing over all paths here—we assume that the path in air from the source to the point of entry into the glass is a straight line, clearly the subpath of stationary phase.
Reflection, Too
Suppose you look at a point of light reflected in a mirror. Imagine the point sending out rays in all directions, as it does. The ray that enters your eye from the mirror goes along the shortest bouncing-off-the-mirror path. You can prove that this is equivalent to angle of incidence equals angle of reflection by considering the path difference for a nearby path.
Of course, for a curved mirror there may be more than one shortest path. To take an extreme case, consider the two-dimensional scenario of a perfectly reflecting ellipse with a point light source inside. If the source is at one focus of the ellipse, all the light will be reflected to the other focus. And, all the paths will have the same length! (Recall an ellipse can be constructed with a piece of string, the ends nailed down at the foci, the string stretched taut.) A parabolic mirror is the limiting case of an ellipse with the other focus sent to infinity, so parallel rays coming in along the axis from a distant star will all go to the focus in phase with each other.
The Bottom Line: Geometric Optics and Wave Optics
In geometric optics, mirrors, lenses, telescopes and so on are analyzed by tracking narrow rays of light through the system, applying the standard rules of reflection and refraction. Despite Huygens’ picture, most people using this well-established technique before 1800 thought the rays were streams of particles. Fermat’s Principle of Least Time was an elegant formulation of the laws of motion of this stream—it reduced all observed deflections, etc., to a single statement. It even included phenomena caused by a variable refractive index, and consequent curved paths for light rays, such as mirages, reflections of distant mountains in the middle-distance ground on hot days caused by a layer of hotter air close to the ground.
But despite its elegance, no theoretical explanation of Fermat’s Principle was forthcoming until it was established that light was a wave—then it became clear. The waves went out over all possible paths, but phase differences caused almost perfect cancellation except for paths in the vicinity of the shortest possible.
We shall find a similar connection between classical mechanics and quantum mechanics.