10. Capacitances
Michael Fowler, University of Virginia
Electrostatics of Systems of Conductors
We know by now that in electrostatic equilibrium, the charges are at rest (by definition of electrostatic!), so, since they are free to move in a conductor, the electric field must be zero inside the conductor, and in fact must be perpendicular to the surface going outward from the conductor into an insulator or vacuum. Therefore, the potential must be constant throughout the conductor.
Capacitance
Let’s start with self-capacitance, think of a single isolated conductor carrying a charge In electrostatic equilibrium the entire conductor will be at the same potential, say, for any in or on the body. (Sorry we also use for volume, but this is standard.)
The self-capacitance (or just capacitance) is defined as
It can be understood as a measure of how much charge can be loaded on the conductor before it reaches a given voltage (potential). Experimentally, the relationship is linear for a rigid conductor over a wide range. The simplest example is the capacitance of an isolated spherical conductor of radius If the sphere has charge its surface is at potential so its capacitance
The SI unit is the farad, the capacitance that increases in potential by one volt when one coulomb of charge is added.
Exercise: what is the radius of a sphere having capacitance one farad?
Grounding a conductor means connecting it via a wire, say, to Earth, so that (in electrostatic equilibrium) it will be at the same potential as the Earth, which we take as our zero. (Reasonably assuming that the Earth itself has no net charge.)

Now imagine we have two conductors, take two spheres, say, both grounded so they are at zero potential. Now remove the connections to Earth, and put a charge on one of them only. What, if anything, happens to the potential of the other (nearby) sphere? It’s helpful to do a qualitative sketch of the electric field lines. The charge on the first sphere will cause some redistribution of charge on the second, so some field lines from the first will end on the second. Furthermore, some field lines will begin on the far side of the second sphere and go to infinity. It is then clear that in fact the second sphere is now at a nonzero potential, it takes work to come in along that field line from infinity. And, as is evident from the linearity, the electrostatic potential, the potential of the second sphere depends linearly on the charge of the first sphere.
The Capacitance Matrix
We’ve defined capacitance for a single conductor as I put that term in because you must have seen it written that way, using the term voltage rather than potential, in earlier courses. However, we’re going to use for potential, not least because we want to use for volume.
We’ll now consider a system of separate conductors, having charges and potentials There are linear connections between the potential on one conductor and the charges on the others, that is, there is a capacitance matrix:
To gain some insight into this expression, consider the following.
Take conductor #1 and use some voltage source to
raise its potential to at the same time have all the other conductors
connected to ground, so all the other potentials are
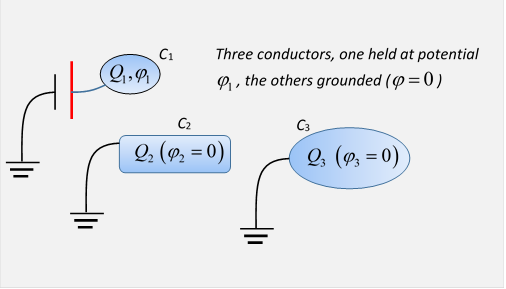 Of course, this means that the charges on
these other conductors will in general be nonzero, the presence of the charge necessary to raise conductor #1 to will attract charges from Earth to the other conductors.
In terms of the capacitance matrix, for
this configuration the conductor has charge
Of course, this means that the charges on
these other conductors will in general be nonzero, the presence of the charge necessary to raise conductor #1 to will attract charges from Earth to the other conductors.
In terms of the capacitance matrix, for
this configuration the conductor has charge
When the charges have come from Earth to the grounded conductors, we can then cut the wires, this will change nothing, as no current was flowing.
We then repeat with all but conductor #2 grounded, #2 being held at and the conductor in this scenario has charge
Repeating the same procedure for all the conductors, each equation is legitimate, and, again invoking linearity, the sums of these solutions (summing both charges and potentials) are also electrostatically valid, therefore unique: the total charge on the conductor when the potentials are set at is
So given any set of potentials on the family of conductors, the capacitance matrix automatically gives us the charge on each conductor. The catch, of course, is in actually evaluating the
Note that the capacitance matrix element is not the self-capacitance of the first conductor if it were in isolation: the charges coming from the ground to the other conductors affect the potential on the first conductor.
Maxwell noticed some other facts about the : obviously the diagonal terms are positive, but equally obviously the off diagonal terms are negative, if I put a positive charge on one conductor it will attract negative charges to the others. If we picture the electric field lines emanating from the one positively charged conductor, in general some of them will end on the other conductors, some will go off to infinity. So, if we put positive charge on one conductor, and the rest are grounded, the total charge on all the conductors is positive or zero.
Another matrix, called the "coefficients of potential" relates the potentials of a set of conductors to the charges they carry:
Substituting we see the matrices are inverses of each other.
The total electrostatic energy is
Forces on Conductors
We've already discussed this: the force on an element of area of a conductor equals the charge on that area multiplied by the electric field there not including the field from the charge element itself. Since there is no electric field inside the conductor, and the local charge density gives a local normal field , the field from the rest must be pointing outwards, and therefore the force outwards. For a single conductor, of course, this force will tend to pull the conductor apart (think a charged soap bubble) but won't move it, since the forces between any two elements are equal and opposite. But with more than one conductor, evidently there will be forces, obviously oppositely charged conductors will attract.
To be specific, consider a parallel plate capacitor, here taken to be two conducting plates, nothing between them (no dielectric) with area much greater than the square of the distance between them, so we can ignore complicated edge effects. Suppose the potential difference is , the charges are . Then the charge density on the plates is and therefore the field strength is . Hence the potential difference is , so the capacitance
The total force on the upper plate is , and attractive, that is,
The total energy in the capacitor is
We can see that separating the plates by an increment takes work . Reassuringly, this is also the change in energy of the capacitor.
Another expression for the total energy in a capacitor is
How does this change on increasing by ?
The change is But the plates attract each other, so we did work. What happened? It went into the battery maintaining the potential, along with some of the energy in the field.
To make this very clear, suppose we just double the (still small) distance between the plates. Since the potential is held constant, this halves the field strength, and since the energy per unit volume goes as the square of the field strength, the field energy in the capacitor has halved. This means the charge density on the plates has halved, that charge had to go somewhere, it went back into the battery: doing work equal to charge lost times .
Exercise: a capacitor has two conducting (but separated) elements, which carry opposite charges. Find the capacitance of two concentric spheres. What is the value if the radii are very close? Do the same for concentric cylinders, per unit length.
The Capacitance Matrix is Symmetric
This follows from the Reciprocation Theorem discussed in the previous lecture.
To put it in words, no matter how weirdly shaped two conductors A and B are, if putting a charge on A raises the potential of B by then putting the same magnitude charge on B raises the potential of A by the same certainly not obvious!
To prove it, consider two conductors C1, C2:
In scenario A,
conductor C1 has charge Q, C2
has charge zero.
 The potentials on the conductors are
The potentials on the conductors are
In scenario B, C1 has charge zero, C2 has charge Q. The potentials are
Applying the Reciprocation Theorem, with only surface charges present,
and noting that on each conductor the potential is constant, so the integrations are trivial, we find immediately