50  Group Velocity and Wave Packet Spread

    Michael Fowler, UVa

Note: The previous lecture finished at the end of section 7.6 of Jackson. Section 7.7 is on magnetohydrodynamic waves: unfortunately, we do not have time to cover this topic here.

Group Velocity: Superposition of Waves in One Dimension

Jackson 7.8

A Wave Packet

Imagine monochromatic laser light passes through a shutter mechanism so a finite train of waves emerges.

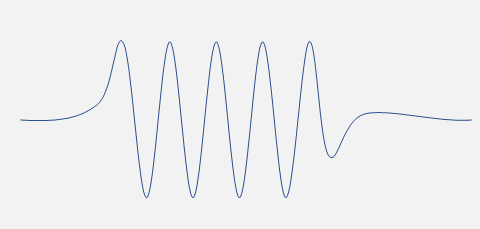
 This wave packet can only be approximately monochromatic, since a true plane wave extends for ever in both directions. The packet amplitude dies away far from the center because slightly different wavelengths eventually get out of sync, and interfere destructively.  If the light is in  vacuum, that's all there is to say, all the slightly different frequency waves move at the same speed, so the packet moves on keeping its shape unchanged.

But in a medium, the permittivity $\epsilon \left(\omega \right)$ in fact varies with frequency, and that means the different frequency components in the wave packet have different phase velocities $v_{\phi }=1/\sqrt{\mu \epsilon },$ so the wave packet itself will change configuration as it progresses.

Adding Two Waves: Phase Velocity and Group Velocity

A localized wave packet needs contributions from a continuum of frequencies, but the most important consequence of refractive index varying with frequency can be found by adding just two waves of slightly different frequencies, this gives a string of "wave packets":

$\sin \left[\left(k+\Delta k\right)x-\left(\omega +\Delta \omega \right)t\right]+\sin \left[\left(k-\Delta k\right)x-\left(\omega -\Delta \omega \right)t\right]=2\sin \left(kx-\omega t\right)\cos \left[\left(\Delta k\right)x-\left(\Delta \omega \right)t\right].$ 

The first term in this product, $\sin \left(kx-\omega t\right),$ is the monochromatic wave, with phase velocity $v_{\phi },$ where

$\omega =v_{\phi }k=\frac{c}{n\left(k\right)}k,$ 

(recall the refractive index $n=\sqrt{\epsilon /{\epsilon }_0},$ and $c=1/\sqrt{{\mu }_0{\epsilon }_0}.$ )  Here we will be taking $\mu ={\mu }_0.$ 

This wave is multiplied by the much more slowly varying second term, called the "envelope", which is moving not at $\omega /k,$ but at $\Delta \omega /\Delta k,$ which will not be the same as the phase velocity if the dielectric constant varies with frequency. Check out the animation!

This envelope speed is termed the group velocity, and written

$v_g=\frac{d\omega }{dk}.$ 

It turns out that this is the speed at which a single quasi-monochromatic wave packet travels, and therefore it is that speed at which the wave delivers energy.

Jackson gives a more general derivation of this result: he assumes a wave packet is made of waves within some narrow range about $k_0,$ in which it is sufficient to take

$$\omega \left(k\right)={\omega }_0+{\left.\frac{d\omega }{dk}\right|}_0\left(k-k_0\right)$$

and expressing the wave packet in terms of its Fourier components for short times near zero

$$u\left(x,t\right)=e^{-i\omega t}{e}^{i{k}_0{\left.\left(d\omega /dk\right)\right|}_{0}t}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}A\left(k\right)e^{i\left[x-{\left.\left(d\omega /dk\right)\right|}_{0}t\right]k}\frac{dk}{2\pi }}.$$

Putting $t=0$ in this expression just gives the wave packet in terms of its Fourier components. Going to nonzero $t$ there is an overall phase factor, but the same Fourier components, now for a wave packet displaced in the $x$-direction by  ${\left.\left(d\omega /dk\right)\right|}_{0}t,$ so the packet is moving at the group velocity in this quasi-monochromatic case.

Differentiating $\omega \left(k\right)=ck/n\left(k\right)$ with respect to $\omega$ gives

$v_g=\frac{c}{n\left(\omega \right)+\omega \left(dn/d\omega \right)}.$ 

Note that in normal dispersion ( $n$ increasing with $\omega$ ) the group velocity is less than the phase velocity $c/n,$ in anomalous dispersion it is greater, and near a resonance things get messy and unreliable.

Other Waves

For quantum electron waves, $\omega =a+b{k}^2,$ the group velocity is twice the phase velocity; for deep water waves, $\omega \propto \sqrt{k},$ it's half the phase velocity, these are gravity waves with pendulum-like frequency-wavelength behavior.

Open the animation and watch the life and death of a single crest within a wave packet! Which end does it disappear at?

To easily observe the group velocity in the animation, cover it with a sheet of paper so that you can only see the tips of the moving wave packets.

We will skip the last part of this section, where Jackson discusses pulse reshaping in regions of anomalous dispersion, where there is resonant absorption, meaning $\epsilon \left(z\right)$ has a pole near the real axis. It is possible to get pulse distortion which gives the impression of faster than light travel, but in fact it’s just that the leading edge can be less attenuated over time than the bulk of the wave packet$—$there is no breakdown of causality.

Spreading of a Pulse as It Propagates in a Dispersive Medium

Jackson 7.9

This section takes a specific example of initial configuration, a Gaussian modulated oscillation

$$u\left(x,0\right)=e^{-x^2/2L^2}\cos k_{0}x,$$

and a particular dispersion relation

$$\omega \left(k\right)=\nu \left(1+\frac{a^2{k}^2}{2}\right).$$

Jackson mentions that this is an approximation to the dispersion of the tenuous plasma (recall we found ${\omega }^2={\omega }_{\text{pl}}^2+c^2{k}^2$ ), but it is also the dispersion relation for a nonrelativistic electron, and this is the  very well-known introductory quantum mechanics problem of the time development of a gaussian wave packet, initially

$$\psi \left(x^{\prime },0,p_0\right)=e^{i{p}_0{x}^{\prime }/\hslash }\frac{e^{-{x^{\prime }}^2/2d^2}}{{\left(\pi d^2\right)}^{1/4}}.$$

This expression is copied from my QM  lecture on Propagators, where the solution is given in full.

Of course, the electromagnetic gaussian pulse is a little bit different, since the electric field has to be real: easily taken care of by writing it as a sum of two terms, $\psi \left(x^{\prime },0,p_0\right)+\psi \left(x^{\prime },0,-p_0\right),$ equal pulses (opposite phase) traveling in opposite directions momentarily coinciding at $t=0.$

The reader can check that Jackson’s final result (7.98) corresponds exactly to the (rearranged) $\psi \left(x,t\right)$ in the Propagator lecture.

previous  index  next