52 Plane Waves in Anisotropic Media

Michael Fowler, UVa

Note: There is no text section in Jackson on this important topic. The student is assumed to figure it out by working through problems 7.16 and 7.17, and also analyzing the ionosphere as an anisotropic medium. The presentation below follows Landau, Continuous Media, p 333. There is a similar treatment in Zangwill.

Introduction

We’ve already discussed one anisotropic medium, the ionosphere. A common anisotropic crystal found in elementary labs is calcite, CaCO₃, whose strange optical properties are readily observed by putting a crystal on top of anything $—$ there is a double image! More spectacularly, a laser beam entering a calcite crystal will be split into two, and two parallel beams come out. In this picture, from Wikipedia, the blue laser light is only visible outside the crystal, from dust particle scattering. (The orange rays are fluoresence inside the crystal.)

Wave Vector and Energy Flow

Suppose we have a monochromatic plane wave in a transparent linear medium having the magnetic properties of the vacuum, but with a non-isotropic permittivity (a 3x3 tensor), that is:

$D_{i} = ε_{i k} E_{k}, \vec{B} = μ_{0} \vec{H} .$

This means that the vector $\vec{D}$ is not, in general, parallel to $\vec{E} .$ Physically, it means the molecules polarize more easily in response to electric fields in particular directions.

Taking all quantities to be proportional to $e^{i (\vec{k} \cdot \vec{r} - ω t)},$ Maxwell's equations

$\dot{\vec{D}} = - \vec{\nabla} \times \vec{H}, \dot{\vec{B}} = \vec{\nabla} \times \vec{E},$

for this plane wave are:

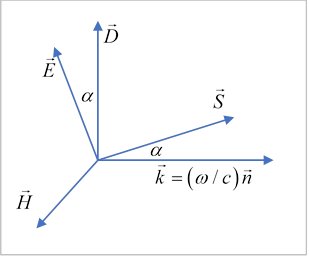
$ω \vec{D} = - \vec{k} \times \vec{H}, ω μ_{0} \vec{H} = \vec{k} \times \vec{E} .$

Staring at these equations, from the first $\vec{D}$ is perpendicular to $\vec{k}$ and $\vec{H},$ and from the second $\vec{H}$ is perpendicular to $\vec{k} .$

That is, $\vec{H}, \vec{k}, \vec{D}$ are all mutually perpendicular: see figure.

Next, $\vec{E}$ is perpendicular to $\vec{H},$ from the second equation, so $\vec{E}$ must be in the $\vec{k}, \vec{D}$ plane.

This means that since $\vec{E}$ is not parallel to $\vec{D},$ $\vec{E}$ is not perpendicular to $\vec{k}$ .

It therefore follows that the direction of energy flow, $\vec{E} \times \vec{H}$ , is not in the same direction as the wave vector $\vec{k}$ !

The Wave Normal Vector

Following Landau, we define the dimensionless "wave normal" vector $\vec{n}$ by

$\vec{k} = \frac{ω}{c} \vec{n} .$

In vacuum, where $ω = c k,$ $\vec{n}$ would be a unit vector, and in an isotropic material, $ω = v k,$ its length would be $\sqrt{ε / ε_{0}} .$ In an anisotropic medium, its length will vary with direction, as we’ll soon see.

The fundamental formulae now become (switching from $\vec{k}$ to $\vec{n}$ )

$c μ_{0} \vec{H} = \vec{n} \times \vec{E}, c \vec{D} = - \vec{n} \times \vec{H} .$

(Notice that $ω$ no longer appears in the equations.)

From these equations: the energy flux Poynting vector can be written in terms of $\vec{E}, \vec{n}$ :

$\vec{S} = \vec{E} \times \vec{H} = \sqrt{ε_{0} / μ_{0}} [E^{2} \vec{n} - (\vec{E} \cdot \vec{n}) \vec{E}] .$

Exercise: Check that for an isotropic material, this gives the correct answer.

The displacement vector $\vec{D}$ can be similarly expressed, using the fundamental formulae above:

$\vec{D} = ε_{0} \vec{n} \times (\vec{E} \times \vec{n}) = ε_{0} [n^{2} \vec{E} - (\vec{n} \cdot \vec{E}) \vec{n}] .$

Now combining this equation with $D_{i} = ε_{i k} E_{k},$ we have:

$(n^{2} δ_{i k} - n_{i} n_{k} - (ε_{i k} / ε_{0})) E_{k} = 0.$

This is a set of three homogeneous simultaneous equations for the components $E_{k}$ , of the form $M x = 0$ . The equations will be self-consistent provided $\det M = 0,$ that is,

$\det |n^{2} δ_{i k} - n_{i} n_{k} - (ε_{i k} / ε_{0})| = 0,$

or, using $k_{i} = n_{i} ω / c, c^{- 2} = μ_{0} ε_{0},$

$|k^{2} δ_{i j} - k_{i} k_{j} - μ_{0} ω^{2} ε_{i j}| = 0.$

In the coordinates where the dielectric tensor is diagonal, with elements $ε^{(x)}, ε^{(y)}, ε^{(z)}$ it is straightforward to write this determinantal equation (in terms of $\vec{n}$ )

$|\begin{matrix} n^{2} - n_{x}^{2} - ε^{(x)} / ε_{0} & - n_{x} n_{y} & - n_{x} n_{z} \\ - n_{x} n_{y} & n^{2} - n_{y}^{2} - ε^{(y)} / ε_{0} & - n_{y} n_{z} \\ - n_{x} n_{z} & - n_{y} n_{z} & n^{2} - n_{z}^{2} - ε^{(z)} / ε_{0} \end{matrix}| = 0.$

For given anisotropic dielectric properties, this tells us what are allowed values of the wave normal vector. These values lie on a surface in the three-dimensional $(n_{x}, n_{y}, n_{z})$ space.

Exercise: Check that this makes sense in the isotropic case, verify the expansion given just below.

Fresnel’s Equation and the Wave Vector Surface

Expanding out the determinant, the condition the equations be consistent becomes:

$\begin{array}{l} ε_{0}^{2} n^{2} (ε^{(x)} n_{x}^{2} + ε^{(y)} n_{y}^{2} + ε^{(z)} n_{z}^{2}) \\ - ε_{0} \{n_{x}^{2} ε^{(x)} (ε^{(y)} + ε^{(z)}) + n_{y}^{2} ε^{(y)} (ε^{(z)} + ε^{(x)}) + n_{z}^{2} ε^{(z)} (ε^{(x)} + ε^{(y)})\} + ε^{(x)} ε^{(y)} ε^{(z)} = 0. \end{array}$

This is Fresnel's equation. In the space spanned by $(n_{x}, n_{y}, n_{z})$ it describes a fourth-order surface, termed the wave vector surface. (There are sixth-order terms in the above expression, but they cancel out.)

Going back momentarily from $\vec{n}$ to $\vec{k},$ and writing this wave vector surface $|k^{2} δ_{i j} - k_{i} k_{j} - μ_{0} ω^{2} ε_{i j}| = 0$ as $f (\vec{k}, ω) = 0,$ (remembering the $ε_{i j}$ may vary with $ω$ as well) makes clear it is the surface of all the vector points $\vec{k}$ corresponding to waves having frequency $ω .$

Group Velocity and Ray Vector

Suppose now a ray of light enters one of these crystals. How does its direction of propagation in the crystal relate to $\vec{n}$ ? (Recall $\vec{k} = c \vec{n} / ω,$ and the wave fields go as $e^{i (\vec{k} \cdot \vec{r} - ω t)} .$ )

The direction of the ray is not $\vec{k},$ because the energy, hence the physical ray, moves at the wave group velocity, ${\vec{v}}_{g} = \partial ω / \partial \vec{k},$ and since the medium is anisotropic, $\vec{v}$ is not in general parallel to $\vec{k} .$

The wave vector surface is $f (\vec{k}, ω) = 0,$ from which

$\frac{\partial f}{\partial ω} \frac{\partial ω}{\partial \vec{k}} + \frac{\partial f}{\partial \vec{k}} = 0,$

and therefore

${\vec{v}}_{g} = \partial ω / \partial \vec{k} = - \frac{\partial f / \partial \vec{k}}{\partial f / \partial ω} = - \frac{{\vec{\nabla}}_{\vec{k}} f (\vec{k}, ω)}{\partial f / \partial ω},$

so the ray direction ${\vec{v}}_{g}$ is that of the normal to the wave vector surface at the given $\vec{k} = (ω / c) \vec{n} .$ (You can check the sign by taking $f = ω - c k$ in 1D.) Landau calls the physical ray direction the ray vector, written $\vec{s},$ and normalizes it by requiring $\vec{n} \cdot \vec{s} = 1.$

Two Refractive Indices

If we take a fixed direction, $\vec{n} = n (\sin θ \cos ϕ, \sin θ \sin ϕ, \cos θ)$ Fresnel's equation becomes a quadratic in $n^{2},$ meaning there are two physical refractive indices, two different wave speeds. How is that possible? It's because different polarizations propagate at different speeds: the electric oscillating field gets different response from the medium depending on the direction it's tugging the molecules.

Uniaxial Crystals

It's all a lot simpler for uniaxial crystals, where (diagonalizing the dielectric matrix) $ε^{(x)} = ε^{(y)} \neq ε^{(z)} .$ Standard notation, in terms of the direction of the axis of symmetry of the crystal, is to write these diagonal elements as $ε_{⊥}, ε_{⊥}, ε_{∥} .$

In this case, the Fresnel equation factors to

$(ε_{0} n^{2} - ε_{⊥}) [ε_{0} ε_{∥} n_{z}^{2} + ε_{0} ε_{⊥} (n_{x}^{2} + n_{y}^{2}) - ε_{⊥} ε_{∥}] = 0.$

This means the wave vector surface becomes two separate surfaces, a sphere and an ellipsoid:

$\begin{array}{l} n^{2} = ε_{⊥} / ε_{0}, \\ \frac{n_{z}^{2}}{ε_{⊥} / ε_{0}} + \frac{n_{x}^{2} + n_{y}^{2}}{ε_{∥} / ε_{0}} = 1. \end{array}$

(Shown here is a negative uniaxial crystal, a positive one also has the ellipsoid touching the sphere at the poles, but the ellipsoid now contains the sphere.)

The wave corresponding to $n^{2} = ε_{⊥} / ε_{0}$ has isotropic index of refraction, so $\vec{D}$ is always parallel to $\vec{E} .$ This is just an ordinary ray: for a given $\vec{k}$ vector pointing to a spot on the spherical surface, the normal to that surface is of course in the same direction, so the group velocity direction coincides with the ray direction.

On the other hand, for the allowed $\vec{k}$ vector on the ellipsoidal surface, the normal to the surface will not be in the direction $\vec{k},$ (except for the axes end points), and the group velocity, the direction of energy transfer, will not be $\vec{k}$ : this is termed the extraordinary ray.

For this uniaxial crystal, the extraordinary ray will be in the plane of the optical axis and the ordinary ray (see figure). (Landau calls this plane the "principal section".) Differentiating the equation for the ellipse,

$\frac{n_{x}}{ε_{∥}} d x + \frac{n_{z}}{ε_{⊥}} d z = 0$

along the ellipse, so the direction of the normal is $(n_{x} / ε_{∥}, n_{z} / ε_{⊥})$ and the direction of the extraordinary ray is therefore given by

$\tan θ^{'} = \frac{ε_{⊥}}{ε_{∥}} \tan θ .$

When a ray of light enters such a crystal, it separates into these two beams, ordinary and extraordinary, having different velocities, and orthogonal polarizations.

Simple Classical Model

To construct a simple classical model having this kind of behavior, assume that the simple harmonic oscillator restoring force potential $- \frac{1}{2} ω_{0}^{2} r^{2}$ in the Lorentz molecule model is replaced by $- \frac{1}{2} ω_{⊥}^{2} (x^{2} + y^{2}) - \frac{1}{2} ω_{∥}^{2} z^{2},$ not unreasonable for modeling the bonds between atoms holding the electrons in place in a non-isotropic lattice having an axis of symmetry.

Now a signal going through the crystal in the direction of the optic axis will have its electric field vector in the $(x, y)$ plane and will have the same speed irrespective of its polarization $—$ all directions in that plane are equivalent. But what about a ray going in along the $x$ axis? If it's polarized along the $z$ axis, $ω_{∥}$ will govern the oscillators’ response. But for polarization along the $y$ axis, $ω_{⊥}$ is what counts. So the two polarizations will travel at different speeds.

This is how a quarter-wave plate works: if linearly polarized light enters, the electric field in the $y z$ plane at 45 degrees to the axis, and the speed difference and plate thickness is such that one component of the polarized ray is delayed a quarter cycle relative to the other on passing through the plate, circularly polarized light will emerge.

previous index next