66  Radiation by an Accelerating Charge

    Michael Fowler, UVa

Introduction

We'll begin with a simple derivation (due to Purcell) of the radiation from a nonrelativistic accelerating charge, and find a simple expression for the power.  We'll then take the simplest possible generalization of this to the relativistic case, to find the central result, the radiation energy loss that determines the limits on accelerator energies for a given size machine.  We'll contrast the results for linear and circular accelerators.  

In the following lecture, we'll confirm the radiation energy result, deriving it from first principles following Lienard and Wiechert, then go on to find the angular distribution of the radiation, of central importance in the actual application of synchrotron radiation, for example.   

Purcell's Derivation of the Larmor Formula

(Actually we gave Landau’s derivation in lecture 57, but Purcell’s gives much more insight into the field behavior.)

For the nonrelativistic case, here's a very elementary derivation due to Purcell.  We take the electric field from a charge in steady motion to be the same as that from a charge at rest (so we're neglecting the previously discussed relativistic strengthening of the field in the perpendicular-to-motion direction.)

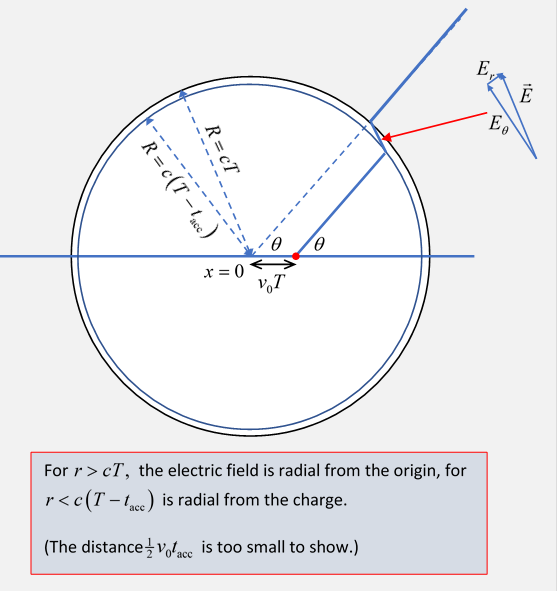
Suppose, then, we have a charge $q$ at rest at the origin for a long time, then, at $t=0,$ say, we apply a  steady force $F$ so the charge undergoes constant acceleration $a=\dot{v}$ for a very short time $t_{\text{acc}}$ up to a speed $v_0=a{t}_{\text{acc}}$ at which point the force cuts out, and the charge from then on moves at this steady speed.  During the acceleration, it will have moved a distance $\frac{1}{2}{v}_0{t}_{\text{acc}}$ (too small to show on the accompanying diagram).

Now consider what the electric field must look like at a much later time $T\gg t_{\text{acc}}.$ At distances greater than $cT$ from the original at rest position of the charge, the subsequent movement of the charge cannot have changed anything, so the electric field out there must still be radial pointing from the origin.  But for distances less than $c\left(T-t_{\text{acc}}\right),$ the radial field lines must emanate from the moving charge. (Recall that we've already established that the field lines from a charge in steady motion are radial from the instantaneous position of the charge: and at distances $r<c\left(T-t_{\text{acc}}\right),$ the field can only depend on the history of the charge after it stopped accelerating.)

So there must be a thin shell, $c\left(T-t_{\text{acc}}\right)<R<cT,$ in which the electric field lines connect.  (The amount of electric field "flowing out" in the cone of angle $\theta$ must be the same before and after, and the electric field lines are continuous at all times.)  $\overrightarrow{E}$ must zigzag as shown, and we see that in the limit of large $R,$ 

$$\frac{E_{\theta }}{E_r}=\frac{v_{0}T\sin \theta }{c{t}_{\text{acc}}}=\frac{v_{0}R\sin \theta }{c^2{t}_{\text{acc}}}.$$  Now, $E_r$ must be essentially the same inside the shell as outside (Gauss' law),

$$E_r=\frac{1}{4\pi {\epsilon }_0}\frac{q}{R^2}.$$  Hence,

$$E_{\theta }=\frac{v_{0}R\sin \theta }{c^2{t}_{\text{acc}}}\cdot \frac{1}{4\pi {\epsilon }_0}\frac{q}{R^2}=\frac{1}{4\pi {\epsilon }_0}\frac{v_0\sin \theta }{c^2{t}_{\text{acc}}}\cdot \frac{q}{R}.$$  That is to say, $E_{\theta }$ goes down with distance only as $1/R.$ Evidently, this is an outgoing electromagnetic wave$—$the same energy propagates outwards independent of the size sphere we take.

We'll take the outgoing radiation to be $P{t}_{\text{acc}},$ the radiation is uniform over a time $t_{\text{acc}},$ so $P$ is the power.  We simply need to find the energy in the electric field in the shell between $T-t_{\text{acc}}$ and $T,$ then remember to double it, because an electromagnetic wave has equal energies in the electric and magnetic fields.

Given the volume of the shell is $4\pi R^{2}c{t}_{\text{acc}}$, and $\overline{{\sin }^2\theta }=\frac{2}{3},$ and putting in $\frac{1}{2}$ because the electric field is only half the wave energy,

$$\begin{array}{c}\frac{1}{2}P{t}_{\text{acc}}={\displaystyle \underset{\text{shell}}{\int }\frac{1}{2}{\epsilon }_0{E}^{2}dV}\\ =\frac{1}{2}{\epsilon }_0\cdot 4\pi R^{2}c{t}_{\text{acc}}\cdot \frac{\frac{2}{3}}{{\left(4\pi {\epsilon }_0\right)}^2}\cdot {\left(\frac{v_{0}R}{c^2{t}_{\text{acc}}}\right)}^2\cdot {\left(\frac{q}{R^2}\right)}^2\\ =\frac{\frac{2}{3}}{4\pi {\epsilon }_0}\cdot \frac{v_0^2}{c^3{t}_{\text{acc}}}\cdot q^2.\end{array}$$   Now we put $v_0=a{t}_{\text{acc}}$ to find

$$P=\frac{1}{4\pi {\epsilon }_0}\cdot \frac{2}{3}\cdot \frac{a^2{q}^2}{c^3}=\frac{1}{6\pi {\epsilon }_0}\cdot \frac{a^2{q}^2}{c^3}=\frac{{\mu }_0}{6\pi }\cdot \frac{a^2{q}^2}{c}.$$  This is called the Larmor formula.

Notice that the power depends on the square of the acceleration, so acceleration in the opposite direction$—$deceleration$—$would emit the same power.  Furthermore, the radiation distribution is obviously azimuthally symmetric about the direction of the acceleration, so the radiated total momentum must be zero.  It follows that on going to a different Lorentz frame, the energy in this shell of radiation increases by a factor $\gamma ,$ as does the time $t_{\text{acc}}$ over which it's emitted, so the power is actually unchanged.

Relativistic Generalization of the Larmor Formula

Deriving the Lienard-Weichert Result

It turns out that the nonrelativistic Larmor formula is not difficult to write as the limit of a relativistic scalar.  Recall that the relativistic four-velocity, $U^{\mu }=d{x}^{\mu }/d\tau ,$ goes to $\left(c,\overrightarrow{v}\right)$ in the nonrelativistic limit, and the four-acceleration $a^{\mu }=d{U}^{\mu }/d\tau =d^2{x}^{\mu }/d{\tau }^2\to \left(0,\overrightarrow{a}\right),$ so the invariant scalar  $a^{\mu }{a}_{\mu }\to {\overrightarrow{a}}^2$.

Hence the obvious generalization to the relativistic case is 

$$P=\frac{{\mu }_0}{6\pi }\cdot \frac{a^{\mu }{a}_{\mu }{q}^2}{c}.$$ This is not a rigorous derivation, there could be other terms in the relativistic expression that go to zero in the nonrelativistic limit.  But from the form of the Lienard Weichert fields, which we cover in the next lecture, the velocity dependence can only be on $\overrightarrow{\beta },\dot{\overrightarrow{\beta }}$ (no higher derivatives) and given this constraint, according to Jackson, this is the only possible relativistic generalization of Larmor's formula.

However, for it to be useful, we need to write this invariant four-acceleration magnitude in terms of ordinary (lab frame) velocities and accelerations, going from proper time to lab time, using

$$\frac{d}{d\tau }=\frac{1}{\sqrt{1-{\beta }^2}}\frac{d}{dt}.$$ Transforming to lab time $t,$ then, and we'll sometimes use a dot to denote differentiation with respect to $t,$ 

$$a^{\mu }=\frac{d^2{x}^{\mu }}{d{\tau }^2}=\frac{1}{\sqrt{1-{\beta }^2}}\frac{d}{dt}\frac{1}{\sqrt{1-{\beta }^2}}\frac{d{x}^{\mu }}{dt},$$ and noting that

$$\dot{\gamma }=\frac{d}{dt}\frac{1}{\sqrt{1-{\beta }^2}}=\frac{\overrightarrow{\beta }\cdot \dot{\overrightarrow{\beta }}}{{\left(1-{\beta }^2\right)}^{3/2}}={\gamma }^3\overrightarrow{\beta }\cdot \dot{\overrightarrow{\beta }},$$ we have

$$\begin{array}{c}{a}^{\mu }=\left(a^0,a^i\right)\\ =\left(\frac{1}{\sqrt{1-{\beta }^2}}\frac{d}{dt}\frac{1}{\sqrt{1-{\beta }^2}}\frac{d\left(ct\right)}{dt},\frac{1}{\sqrt{1-{\beta }^2}}\frac{d}{dt}\frac{1}{\sqrt{1-{\beta }^2}}\frac{d{x}^i}{dt}\right)\\ =c\left(\gamma \dot{\gamma },\gamma \dot{\gamma }{\beta }^i+{\gamma }^2{\dot{\beta }}^i\right),\end{array}$$ Then, using (from the previous equation) $\dot{\gamma }={\gamma }^3\overrightarrow{\beta }\cdot \dot{\overrightarrow{\beta }}$ to eliminate $\dot{\gamma },$ we find

$$a^{\mu }=\left(a^0,a^i\right)=c{\gamma }^2\left({\gamma }^2\left(\beta \cdot \dot{\beta }\right),{\gamma }^2{\beta }^i\left(\beta \cdot \dot{\beta }\right)+{\dot{\beta }}^i\right).$$ Hence

$$\begin{array}{c}\left(a^{\mu }{a}_{\mu }\right)/c^2{\gamma }^4=-{\gamma }^4{\left(\beta \cdot \dot{\beta }\right)}^2+{\gamma }^4{\beta }^2{\left(\beta \cdot \dot{\beta }\right)}^2+2{\gamma }^2{\left(\beta \cdot \dot{\beta }\right)}^2+{\dot{\beta }}^2\\ =-{\gamma }^4\left(1-{\beta }^2\right){\left(\beta \cdot \dot{\beta }\right)}^2+2{\gamma }^2{\left(\beta \cdot \dot{\beta }\right)}^2+{\dot{\beta }}^2\\ =-{\gamma }^2{\left(\beta \cdot \dot{\beta }\right)}^2+2{\gamma }^2{\left(\beta \cdot \dot{\beta }\right)}^2+{\dot{\beta }}^2\\ ={\gamma }^2\left[\left(1-{\beta }^2\right){\dot{\beta }}^2+{\left(\beta \cdot \dot{\beta }\right)}^2\right]\\ ={\gamma }^2\left[{\dot{\beta }}^2-{\left(\beta \times \dot{\beta }\right)}^2\right].\end{array}$$ So the power

$$P=\frac{{\mu }_{0}c{q}^2{\gamma }^6}{6\pi }\left[{\dot{\beta }}^2-{\left(\beta \times \dot{\beta }\right)}^2\right]=\frac{2}{3}\cdot \frac{1}{4\pi {\epsilon }_0}\cdot \frac{q^2{\gamma }^6}{c}\cdot \left[{\dot{\beta }}^2-{\left(\beta \times \dot{\beta }\right)}^2\right].$$ This is the famous result of Lienard and Weichert, presented by Jackson in terms of the momentum of a charged particle:

$$P=\frac{2}{3}\frac{1}{4\pi {\epsilon }_0}\frac{q^2}{m^2{c}^3}\left(\frac{d{p}_{\mu }}{d\tau }\cdot \frac{d{p}^{\mu }}{d\tau }\right).$$ Exercise: Write the nonrelativistic Larmor formula for an accelerating charged particle in terms of the rate of change of particle momentum, then find this formula as the relativistic generalization.

Jackson remarks that the appearance of mass in the denominator here means radiation power loss is far more serious for electrons than for protons, which is of course true, but the radiation doesn't depend on the mass of the particle, this is not gravitational radiation, the point is that for a given speed and acceleration the radiation from an electron is the same as for a proton: the radiation is of course from the electric charge, the mass of its carrier is irrelevant.

That being said, the energy of a  particle $E=\gamma m{c}^2$, so for an electron and a proton of equal energy $E$, say a one Gev electron and a one Gev proton, we have ${\gamma }_e{m}_e={\gamma }_p{m}_p,$ so the energy loss for the electron (notice the ${\gamma }^6$ in the expression for $P$ ) is far greater.  (As we'll soon see, it drops to ${\gamma }^4$ in circular motion, but that's still very large.)

Linear Accelerator

For a particle traveling along a straight line and accelerating, $\overrightarrow{\beta }\times \dot{\overrightarrow{\beta }}=0$ so the rate of energy radiation

$$\begin{array}{c}P=\frac{2}{3}\cdot \frac{1}{4\pi {\epsilon }_0}\cdot \frac{q^2{\gamma }^6}{c}\cdot {\dot{\beta }}^2\\ =\frac{2}{3}\cdot \frac{1}{4\pi {\epsilon }_0}\cdot \frac{q^2}{m^2{c}^3}{\left(\frac{dp}{dt}\right)}^2.\end{array}$$ That last line, connecting with Jackson, uses $\dot{\gamma }={\gamma }^3\overrightarrow{\beta }\cdot \dot{\overrightarrow{\beta }}={\gamma }^3\beta \dot{\beta }$  and from $p=\gamma mc\beta$and $\dot{\gamma }={\gamma }^3\overrightarrow{\beta }\cdot \dot{\overrightarrow{\beta }},$ we have $$\dot{p}=\dot{\gamma }mc\beta +\gamma mc\dot{\beta }={\gamma }^{3}mc\dot{\beta }{\beta }^2+{\gamma }^3\left(1-{\beta }^2\right)mc\dot{\beta }={\gamma }^{3}mc\dot{\beta }.$$ 

Using that the accelerating force $\left(dp/dt\right)=\left(dE/dx\right)$ we find:

$$P=\frac{2}{3}\frac{1}{4\pi {\epsilon }_0}\frac{q^2}{m^2{c}^3}{\left(\frac{dE}{dx}\right)}^2.$$ This means the rate of radiative energy loss in linear motion depends only on the external force that determines the change of particle energy with distance$—$not on the particle's actual energy.

So the ratio of radiative energy loss to power being supplied is

$$\frac{P}{\left(dE/dt\right)}=\frac{2}{3}\frac{1}{4\pi {\epsilon }_0}\frac{q^2}{m^2{c}^3}\frac{1}{v}\frac{dE}{dx}\underset{v\to c}{\to }\frac{2}{3}\frac{1}{4\pi {\epsilon }_0}\frac{\left(q^2/m{c}^2\right)}{m{c}^2}\frac{dE}{dx}.$$ For an electron, the length $\frac{1}{4\pi {\epsilon }_0}\frac{q^2}{m{c}^2}$ is called the classical radius (for the charge confined to this radius, the electric field energy is the rest mass) and is of order 10^-15 meters.  In a real linear accelerator, essentially no energy is gained in that distance, so radiative energy loss is not a problem.

Circular Accelerator

This time ${\left(\beta \times \dot{\beta }\right)}^2={\beta }^2{\dot{\beta }}^2$ so

$$P=\frac{2}{3}\cdot \frac{1}{4\pi {\epsilon }_0}\cdot \frac{q^2{\gamma }^6}{c}\left[{\dot{\beta }}^2-{\left(\beta \times \dot{\beta }\right)}^2\right]=\frac{2}{3}\cdot \frac{1}{4\pi {\epsilon }_0}\cdot \frac{q^2{\gamma }^4}{c}{\dot{\beta }}^2,$$ and in terms of momentum, since $\dot{p}=\gamma mc\dot{\beta }$ for sideways acceleration,

$$P=\frac{2}{3}\cdot \frac{1}{4\pi {\epsilon }_0}\cdot \frac{q^2{\gamma }^2}{m^2{c}^3}{\left(\frac{dp}{dt}\right)}^2,$$  so for going in a circle of radius $r,$ for which $\dot{\beta }=c{\beta }^2/r,$ 

$$P=\frac{2}{3}\cdot \frac{c{q}^2{\gamma }^4}{4\pi {\epsilon }_0}\cdot \frac{{\beta }^4}{r^2}.$$ Note that this doesn’t depend on the mass of the particle$—$of course$—$it’s from the accelerating charge. But the total energy is $E=\gamma m{c}^2,$ so the power loss is far more serious for electrons than for protons.

The energy loss per revolution is

$$\delta E=\frac{2\pi r}{c\beta }P=\frac{2\pi r}{c\beta }\frac{2}{3}\cdot \frac{c{q}^2{\gamma }^4}{4\pi {\epsilon }_0}\cdot \frac{{\beta }^4}{r^2}=\frac{1}{3{\epsilon }_0}\cdot \frac{{\gamma }^4{\beta }^4}{r}.$$ and in numbers (from Jackson)

$$\delta E\left(\text{MeV}\right)=8.85\times {10}^{-2}\frac{{\left[E\left(\text{GeV}\right)\right]}^4}{r\left(\text{meters}\right)}.$$ For the Cornell electron synchrotron, a 10 GeV machine with a radius of 100 meters, loss per turn at maximum design energy is 8.85 MeV, energy supplies is 10 MeV.

previous  index  next