previous  index  next 

35  Faraday’s Law of Induction

    Michael Fowler, UVa

Beginnings…

In 1820, Oersted in Denmark noticed that a compass needle moved when he connected a battery to a nearby wire. This was the first clue that electricity and magnetism were related.  Faraday discussed this observation with Oersted, then went on to several years of experimentation on the effect.

 

He discovered that a changing magnetic field induces a temporary current in a loop of wire, magnified by replacing the loop with a coil of many loops. In 1831, he carried out the experiment depicted here, the magnet is now an electromagnet (the smaller coil), the changing magnetic field is achieved by either moving the magnet or by switching its current on or off. 

The cylinder on the right is the battery, that on the left is the galvanometer detecting current in the outer coil.

Faraday’s Result: the Law of Induction

After many experiments with this and other devices, Faraday concluded that, to take the case of a single loop of wire, changing the magnetic flux through the loop caused the current, meaning that if the wire is roofed with an (imaginary) surface, the rate of change of the total magnetic flux through the surface:

$$\frac{dF}{dt}=\frac{d}{dt}{\displaystyle \int \overrightarrow{B}\cdot \widehat{\overrightarrow{n}}da,}$$

is the relevant parameter.

(Since $\overrightarrow{\nabla }\cdot \overrightarrow{B}=0$ always, any surface with edges along the loop will do.) 

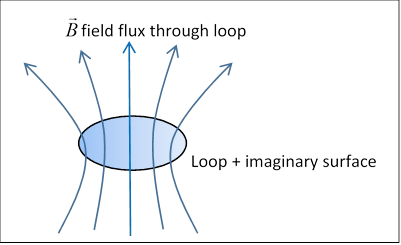
Since a current is generated in the closed loop of wire, evidently the changing magnetic flux creates a momentary nonconservative electric field:

${\displaystyle \underset{C}{\oint }\overrightarrow{E}\cdot d\overrightarrow{l}}=ℰ\ne 0.$

$ℰ$ is called the electromotive force, it's the total voltage generated around the circuit. 

(This term, usually shortened to emf, was originally used as a measure of battery output voltage.)

Experimentally, Faraday found the emf $ℰ$ around the loop was proportional to the rate of change of magnetic flux through the loop, his Law of Induction:

$$ℰ=-k\frac{dF}{dt}.$$  (Obviously $k$ depends on the units of magnetic field and voltage.)

Determining Faraday's k:  Is Moving the Magnet the Same as Moving the Coil?

Let's consider a particular example: suppose we have a loop of wire, and a permanent magnet, so that if the magnet is stationary, the field isn't changing.  Now suppose that in a short time $\delta t$ the magnet moves a small distance $\delta \overrightarrow{r}.$  How does that affect the magnetic flux through the coil?

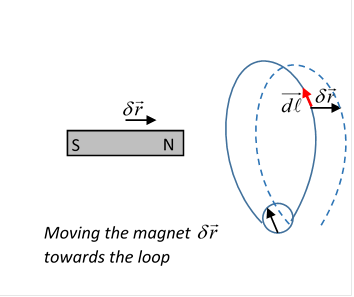
Imagine the field as Faraday did, lines or tubes of field sprouting out of the magnet. When we move the magnet, all this moves with it.  If we just move the magnet a short distance $\delta \overrightarrow{r}$, some of the field lines that were threading through the loop now pass outside it, or vice versa.

But how much field flux total goes from inside to outside?  Consider one infinitesimal bit of the wire, $\overrightarrow{dl}$ (the little red arrow).   If the whole field moves by $\delta \overrightarrow{r},$ the field that crosses this bit of wire during the move is that through an area $\overrightarrow{dl}\times \delta \overrightarrow{r},$ that is, a flux change $\overrightarrow{dl}\times \delta \overrightarrow{r}\cdot \overrightarrow{B}.$ 

Therefore, the total change of flux through the loop $\delta F$ as the magnet is moved through $\delta \overrightarrow{r}$ is that through the area (like a collar!) based on the loop, see the figure,

$$\delta F={\displaystyle \underset{C}{\oint }\overrightarrow{dl}\times \delta \overrightarrow{r}\cdot \overrightarrow{B}}.$$  Suppose now this move $\delta \overrightarrow{r}$ takes place in a time $\delta t,$ then take the infinitesimal limit, to get

$$\frac{dF}{dt}={\displaystyle \underset{C}{\oint }\overrightarrow{dl}\times \overrightarrow{v}\cdot \overrightarrow{B}}.$$  Hence by analyzing what happens when we move the magnet, we've found we can formulate Faraday's experimental finding as

$$ℰ=-k\frac{dF}{dt}=-k{\displaystyle \underset{C}{\oint }\overrightarrow{dl}\times \overrightarrow{v}\cdot \overrightarrow{B}}.$$  To put this into words:  we have a coil at rest.  When we move the magnet, the moving magnetic field generates a non-conservative electric field which drives a current around the coil, and the effective voltage, the emf, is given by the equation above, which comes from experiment.

But what if we'd moved the coil instead of the magnet?  Then the magnet and its field being stationary, the fact that a moving magnetic field generates an electric field is irrelevant!  There are no electric fields this time. 

So, is there a current in the coil or not?  Of course there is.  But why?  To see the answer, consider a charge at rest in the wire. Give the wire a velocity $\overrightarrow{v}.$ Now the charge is moving at velocity $\overrightarrow{v}$ through the magnetic field, and so will feel the Lorentz force $q\overrightarrow{v}\times \overrightarrow{B}.$ This will generate a potential drop along an infinitesimal piece of the wire of length $dl$ equal to $\overrightarrow{v}\times \overrightarrow{B}\cdot \overrightarrow{dl}$ for a total potential around the loop of

$${ℰ}^{ \text{'}}={\displaystyle \underset{C}{\oint }\overrightarrow{v}\times \overrightarrow{B}\cdot \overrightarrow{dl}}$$  Notice that

$${ℰ}^{ \text{'}}=ℰ$$  only if $k=1.$ So that fixes $k.$ 

(Perhaps we should mention that Faraday found $k=1$ (for our standard units) experimentally, and the derivation above depends on knowing the Lorentz force on a charge, first written down by Heaviside in the 1880's, long after Faraday, although known indirectly much earlier, from forces between current-carrying wires.)

The standard analysis presented here troubled Einstein: in one frame the charges are being propelled by an electric field generated by the changing magnetic field, in the other by the Lorentz force from the static magnetic field.  The early thinking here was that there was an absolute rest frame, and these were different phenomena.  But Einstein was (rightly) convinced that these were one and the same phenomenon, and one observer's electric field had to be at least partially a magnetic field in a relatively moving frame.  Of course, we’ll return to this later, when we do relativity.

A Maxwell Equation

From Stokes’ theorem, and now putting $k=1,$ the differential form of Faraday’s law is

$$\overrightarrow{\nabla }\times \overrightarrow{E}=-\frac{\partial \overrightarrow{B}}{\partial t}.$$

Lenz' Law

The direction of the current induced by a changing magnetic field can always be deduced using Lenz' law, which is that the system tends to oppose the relative motion of wire and magnet.  This must be true from energy conservation: if energy is being fed into the current, work is being done, so the motion of the magnet must be against a force, the system is resisting the change in magnetic field threading the circuit. So Faraday discovered the Third Maxwell Equation$—$although it took Maxwell to write it mathematically.

Exercise: Would the argument change if the loop has extremely low resistance and there is a current in it before the magnet is moved?

Reading Assignment:  It’s always worth reading Feynman’s notes, maybe you read them as an undergraduate, but look over them again!

previous  index  next