previous  index  next 

20.  Green's Functions in Spherical Coordinates: Constructing an Image

    Michael Fowler, UVa

Preliminaries: Single Point Charge

As an example of using spherical harmonics in electrostatics, we’ll take another look at the old favorite of a point charge outside a grounded conducting sphere, and show how simple considerations of symmetry lead automatically to the image.

Let's begin with the single point charge.  The Green's function

$$G\left(\overrightarrow{r},{\overrightarrow{r}}^{\prime }\right)=\frac{1}{\left|\overrightarrow{r}-{\overrightarrow{r}}^{\prime }\right|},$$

is the solution of

${\nabla }^{2}G\left(\overrightarrow{r},{\overrightarrow{r}}^{\prime }\right)=-4\pi \delta \left(\overrightarrow{r}-{\overrightarrow{r}}^{\prime }\right),$

that is, it's the potential $\phi \left(\overrightarrow{r}\right)$ from a unit charge at ${\overrightarrow{r}}^{\prime }.$ 

To translate to spherical coordinates, recall from the Spherical Harmonics lecture that, in terms of the angle between the two vectors and of their spatial orientation,

$\frac{1}{\left|\overrightarrow{r}-{\overrightarrow{r}}^{\prime }\right|}={\displaystyle \sum _{\ell =0}^{\infty }\frac{r_{<}^{\ell }}{r_{>}^{\ell +1}}{P}_{\ell }\left(\cos \gamma \right)}=4\pi {\displaystyle \sum _{\ell =0}^{\infty }\frac{1}{2\ell +1}\frac{r_{<}^{\ell }}{r_{>}^{\ell +1}}{\displaystyle \sum _{m=-\ell }^{\ell }{Y}_{\ell }^m*\left({\theta }^{\prime },{\varphi }^{\prime }\right)Y_{\ell }^m\left(\theta ,\varphi \right)},}$

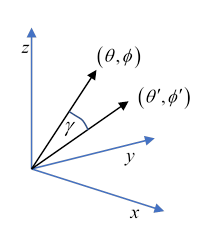
where $r_{>},r_{<}$ are the greater and lesser of $r,r^{\prime }.$ 

It’s important to realize that the last term is symmetric in $r,r^{\prime }$ (as it must be) even though it’s not symmetric in $r_{>},r_{<}$ because swapping $r,r^{\prime }$ changes which one is $r_{>}.$

But how can we see the expression on the right is a solution to ${\nabla }^{2}G\left(\overrightarrow{r},{\overrightarrow{r}}^{\prime }\right)=-4\pi \delta \left(\overrightarrow{r}-{\overrightarrow{r}}^{\prime }\right)$ ?

First we need the delta function itself in spherical coordinates.

Now

$1={\displaystyle \int d^{3}r\delta \left(\overrightarrow{r}-{\overrightarrow{r}}^{\prime }\right)}={\displaystyle \int r^{2}dr\sin \theta d\theta d\varphi }\delta \left(\overrightarrow{r}-{\overrightarrow{r}}^{\prime }\right),$

and $\delta \left(\cos {\theta }^{\prime }-\cos \theta \right)=\left(1/\sin \theta \right)\delta \left(\theta -{\theta }^{\prime }\right),$ so

$\delta \left(\overrightarrow{r}-{\overrightarrow{r}}^{\prime }\right)=\frac{1}{r^2}\delta \left(r-r^{\prime }\right)\delta \left(\cos {\theta }^{\prime }-\cos \theta \right)\delta \left({\varphi }^{\prime }-\varphi \right).$

Furthermore,   

${\displaystyle \sum _{\ell =0}^{\infty }{\displaystyle \sum _{m=-\ell }^{\ell }{Y}_{\ell }^m*\left({\theta }^{\prime },{\varphi }^{\prime }\right)Y_{\ell }^m\left(\theta ,\varphi \right)}}=\delta \left(\varphi -{\varphi }^{\prime }\right)\delta \left(\cos \theta -\cos {\theta }^{\prime }\right).$

(This completeness is nontrivial to prove: the functions are all the eigenstates of the Laplacian on the spherical surface,  $Y_{\ell }^m$ having eigenvalue $-\ell \left(\ell +1\right)$.)

Except on the shell $r=r^{\prime },$ the radial component of the ${\nabla }^2$ operator multiplies the ${\ell }^{\text{th}}$ term in the expression by $+\ell \left(\ell +1\right),$ giving the (full operator) result ${\nabla }^2\phi =0,$ as we expect.

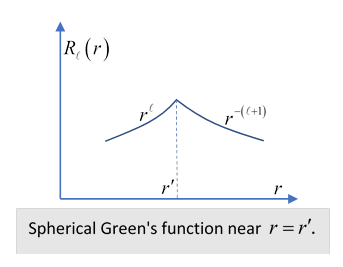
However, at $r=r^{\prime }$ the slope of the ${\ell }^{\text{th}}$ radial function (putting $r_{<}=r_{>}$ after differentiating) changes by

$\frac{1}{2\ell +1}\left(-\left(\ell +1\right)-\ell \right)\frac{1}{r^2}=-\frac{1}{r^2}.$

Notice this is independent of $\ell .$ The radial part of the ${\nabla }^2$ operator can be written $\frac{d^{2}R}{d{r}^2}+\frac{2}{r}\frac{dR}{dr}$ and this change in slope yields on differentiation $-\frac{1}{r^2}\delta \left(r-r^{\prime }\right).$ 

So ${\nabla }^2\phi$ has the same radial shell of delta function in each term, but this is to be multiplied by the angular term, then summing the series gives the angular delta function, leaving nonzero only the point on the shell $\left(\theta ,\varphi \right).$ This recovers the full three-dimensional delta function in spherical polars:

$-4\pi \delta \left(\overrightarrow{r}-{\overrightarrow{r}}^{\prime }\right)=-\frac{4\pi }{r^2}\delta \left(r-r^{\prime }\right)\delta \left(\cos {\theta }^{\prime }-\cos \theta \right)\delta \left({\varphi }^{\prime }-\varphi \right).$

Adding the Grounded Spherical Conductor

The trivial example described above had no boundary conditions.  Consider the same problem, a single point charge at distance $r^{\prime }$ from the origin, but now there is a grounded conducting sphere of radius $a<r^{\prime }$ centered at the origin.

The angular structure will be the same as for the single point charge analyzed above, but the function in $a<r<r^{\prime }$ will have both positive and negative powers of $r,$ cancelling at $r=a.$ 

The Green’s function must have the spherical harmonic series from the point charge we’ve already found, but each term in the series must now have an $r_{<}^{-\left(\ell +1\right)}$ term added to the $r_{<}^{\ell }$ term, to ensure the potential vanishes at the grounded conducting surface, $r=a.$ Furthermore, these new terms must also vanish if $a=0,$ and finally they must have the Green’s function symmetry in $r,r^{\prime }.$

Putting all these requirements together, and adjusting the power of $a$ to get the dimensions correct, we find

$$G\left(\overrightarrow{r},{\overrightarrow{r}}^{\prime }\right)=4\pi {\displaystyle \sum _{\ell =0}^{\infty }\frac{1}{2\ell +1}\left(\frac{r_{<}^{\ell }}{r_{>}^{\ell +1}}-\frac{a^{2\ell +1}}{r_{<}^{\ell +1}{r}_{>}^{\ell +1}}\right){\displaystyle \sum _{m=-\ell }^{\ell }{Y}_{\ell }^m*\left({\theta }^{\prime },{\varphi }^{\prime }\right)Y_{\ell }^m\left(\theta ,\varphi \right)}}.$$

Note now that since the second term is symmetric in $r_{>},r_{<}$ we can replace them with $r,r^{\prime },$ and slightly rearrange to find

$G\left(\overrightarrow{r},{\overrightarrow{r}}^{\prime }\right)=4\pi {\displaystyle \sum _{\ell =0}^{\infty }\frac{1}{2\ell +1}\left(\frac{r_{<}^{\ell }}{r_{>}^{\ell +1}}-\frac{a}{r^{\prime }}\frac{{\left(a^2/r^{\prime }\right)}^{\ell }}{r^{\left(\ell +1\right)}}\right){\displaystyle \sum _{m=-\ell }^{\ell }{Y}_{\ell }^m*\left({\theta }^{\prime },{\varphi }^{\prime }\right)Y_{\ell }^m\left(\theta ,\varphi \right)}}.$

The first term is identical to the potential from a single charge found in the previous section, the second term has the same form: but now the charge is $-a/r^{\prime }$ instead of one, and the position is $a^2/r^{\prime }$ instead of $r^{\prime },$ but along the same axis.  In other words, we've found the image charge the hard way!

Green’s Function Inside Grounded Hollow Conducting Sphere

It is straightforward to adjust the above analysis to this scenario:  consider first the region $0<r^{\prime }<r<a.$ Here

$$G\left(\overrightarrow{r},{\overrightarrow{r}}^{\prime }\right)=4\pi {\displaystyle \sum _{\ell =0}^{\infty }\frac{1}{2\ell +1}\left(\frac{{r^{\prime }}^{\ell }}{r^{\ell +1}}-\frac{{r^{\prime }}^{\ell }{r}^{\ell }}{a^{2\ell +1}}\right){\displaystyle \sum _{m=-\ell }^{\ell }{Y}_{\ell }^m*\left({\theta }^{\prime },{\varphi }^{\prime }\right)Y_{\ell }^m\left(\theta ,\varphi \right)}},$$

clearly going to zero at $r=a.$

Rearranging:

$$G\left(\overrightarrow{r},{\overrightarrow{r}}^{\prime }\right)=4\pi {\displaystyle \sum _{\ell =0}^{\infty }\frac{1}{2\ell +1}\left(\frac{{r^{\prime }}^{\ell }}{r^{\ell +1}}-\frac{a}{r^{\prime }}\frac{r^{\ell }}{{\left(a^2/r^{\prime }\right)}^{\ell +1}}\right){\displaystyle \sum _{m=-\ell }^{\ell }{Y}_{\ell }^m*\left({\theta }^{\prime },{\varphi }^{\prime }\right)Y_{\ell }^m\left(\theta ,\varphi \right)}}.$$

The second term is the potential from a charge equal to $-\left(a/r^{\prime }\right)$ at radius $\left(a^2/r^{\prime }\right)$ on the radial line of the original charge$—$the image is bigger, it’s a concave mirror.

Poisson’s Formula and the Green’s Function

Suppose there is an electric potential, but no electric charge, in a sphere of radius $a$ centered at the origin. Then, inside the sphere, we can expand the potential in spherical harmonics, but only those nonsingular at the origin:

$$\phi \left(\overrightarrow{r}\right)=4\pi {\displaystyle \sum _{\ell =0}^{\infty }{r}^{\ell }{\displaystyle \sum _{m=-\ell }^{\ell }{a}_{\ell m}{Y}_{\ell }^m\left(\theta ,\varphi \right)}}.$$

Poisson showed that if we know the potential everywhere on the spherical surface $r=a,$ call it $V\left(a,\theta ,\varphi \right),$ then we can find it anywhere within the sphere.

The essential point is that this knowledge uniquely determines the coefficients $a_{\ell m}:$ from the orthonormality relation we find

So Poisson’s formula for the potential anywhere inside the sphere is:

How does this relate to the Green’s function in this space? Recall that from the Reciprocation Theorem, if there is zero charge within the sphere, and you know the potential everywhere on the spherical surface, then the potential at any inside point is given by integrating over the spherical surface the normal derivative of the Green’s function from that point, that is (remembering that the normal points into the space)

$$\phi \left(r,\theta ,\varphi \right)=-\frac{1}{4\pi }{\displaystyle \int a^{2}d{\varphi }^{\prime }\sin {\theta }^{\prime }d{\theta }^{\prime }{\left(\frac{d}{d{r}^{\prime }}\right)}_{r^{\prime }=a}}G\left(r,\theta ,\varphi ;r^{\prime },{\theta }^{\prime },{\varphi }^{\prime }\right)V\left({\theta }^{\prime },{\varphi }^{\prime }\right).$$

Now, the Green’s function in the region $r^{\prime }>r,$ (true for $r^{\prime }=a$ ) is

$$G\left(\overrightarrow{r},{\overrightarrow{r}}^{\prime }\right)=4\pi {\displaystyle \sum _{\ell =0}^{\infty }\frac{1}{2\ell +1}\left(\frac{r^{\ell }}{{\left(r^{\prime }\right)}^{\ell +1}}-\frac{{r^{\prime }}^{\ell }{r}^{\ell }}{a^{2\ell +1}}\right){\displaystyle \sum _{m=-\ell }^{\ell }{Y}_{\ell }^m*\left({\theta }^{\prime },{\varphi }^{\prime }\right)Y_{\ell }^m\left(\theta ,\varphi \right)}},$$

so, differentiating with respect to $r^{\prime },$ then putting $r^{\prime }=a,$ 

$${\left(\frac{\partial G\left(\overrightarrow{r},{\overrightarrow{r}}^{\prime }\right)}{\partial r^{\prime }}\right)}_{r^{\prime }=a}=-4\pi {\displaystyle \sum _{\ell =0}^{\infty }{\left(\frac{r}{a}\right)}^{\ell }\frac{1}{a^2}{\displaystyle \sum _{m=-\ell }^{\ell }{Y}_{\ell }^m*\left({\theta }^{\prime },{\varphi }^{\prime }\right)Y_{\ell }^m\left(\theta ,\varphi \right)}},$$

and putting this in the expression for the potential,

$$\phi \left(r,\theta ,\varphi \right)={\displaystyle \int d{\varphi }^{\prime }\sin {\theta }^{\prime }d{\theta }^{\prime }}{\displaystyle \sum _{\ell =0}^{\infty }{\left(\frac{r}{a}\right)}^{\ell }{\displaystyle \sum _{m=-\ell }^{\ell }{Y}_{\ell }^m*\left({\theta }^{\prime },{\varphi }^{\prime }\right)Y_{\ell }^m\left(\theta ,\varphi \right)}}V\left({\theta }^{\prime },{\varphi }^{\prime }\right),$$

identical to Poisson’s result.

More General Spherical Green's Function Problems

This method will work for situations where the image technique is much messier.  For example, suppose the charge is between two grounded conducting concentric spheres, so $a<r,r^{\prime }<b.$  This will need an infinite series of images. But by the present method, it is straightforward.  In the two regions, both positive and negative powers of $r$ are present. The boundary conditions are simple: the radial Green’s function must vanish when $r_{<}=a$ or $r_{>}=b,$ so (Jackson 3.122)

$$g_{\ell }\left(r,r^{\prime }\right)=C\left(r_{<}^{\ell }-\frac{a^{2\ell +1}}{r_{<}^{\ell +1}}\right)\left(\frac{1}{r_{>}^{\ell +1}}-\frac{r_{>}^{\ell }}{b^{2\ell +1}}\right),$$

 and the constant $C$ is determined by the radial Green's function change of slope at $r=r^{\prime }$ 

$${\left(\frac{d{g}_{\ell }\left(r,r^{\prime }\right)}{dr}\right)}_{r=r^{\prime }+\epsilon }-{\left(\frac{d{g}_{\ell }\left(r,r^{\prime }\right)}{dr}\right)}_{r=r^{\prime }-\epsilon }=-\frac{4\pi }{{r^{\prime }}^2}.$$

(Note:  Jackson works with $rg$ rather than just $g$ for some reason, but the equations are equivalent, the result is the same.)

This gives

$$C=\frac{4\pi }{\left(2\ell +1\right)\left(1-{\left(a/b\right)}^{2\ell +1}\right)}.$$

Exercise:  Prove it.

previous  index  next